
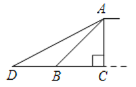
【题目】某市为了缓解城市交通压力,决定修建人行天桥,原设计天桥的楼梯与地面的夹角为45°(∠ABC=45°),BC=4.2 m,后考虑安全因素,将楼梯角B移到CB的延长线上点D处,使∠ADC=23°(如图所示).求BD的长(精确到0.1 m).(参考数据:sin 67°≈0.92,cos 67°≈0.39,tan 67°≈2.36)
科目:初中数学 来源: 题型:
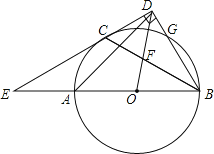
【题目】如图:AB是⊙O的直径,C、G是⊙O上两点,且点C是劣弧AG的中点,过点C的直线CD⊥BG的延长线于点D,交BA的延长线于点E,连接BC,交OD于点F.
(1)求证:CD是⊙O的切线;
(2)若ED=![]() DB,求证:3OF=2DF;
DB,求证:3OF=2DF;
(3)在(2)的条件下,连接AD,若CD=3,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
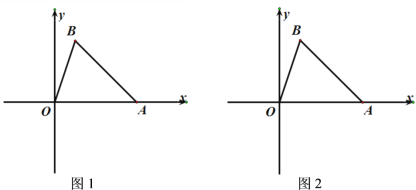
【题目】在平面直角坐标系xoy中,已知 A(4,0)、B(1,3), 过![]() 的直线
的直线![]() 是绕着△OAB的顶点A旋转,与y轴相交于点P,探究解决下列问题:
是绕着△OAB的顶点A旋转,与y轴相交于点P,探究解决下列问题:
(1)如图1所示,当直线![]() 旋转到与边OB相交时,试用无刻度的直尺和圆规确定点P的位置,使顶点O、B到直线
旋转到与边OB相交时,试用无刻度的直尺和圆规确定点P的位置,使顶点O、B到直线![]() 的距离之和最大,(保留作图痕迹);
的距离之和最大,(保留作图痕迹);
(2)当直线![]() 旋转到与y轴的负半轴相交时,使顶点O、B到直线
旋转到与y轴的负半轴相交时,使顶点O、B到直线![]() 的距离之和最大,请直接写出点P的坐标是 .(可在图2中分析)
的距离之和最大,请直接写出点P的坐标是 .(可在图2中分析)
查看答案和解析>>
科目:初中数学 来源: 题型:
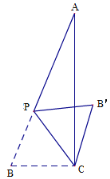
【题目】如图,在△ABC 中,∠ACB=90°,AC=12,BC=5,P 是边 AB 上的动点(不与点 B 重合),将△BCP 沿 CP 所在的直线翻折,得到△B'CP,连接 B'A,B'A 长度的最小值是 m,B'A 长度的最大值是 n,则 m+n 的值等于 ______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线y=x+2经过点A(m,-2),将点A向右平移7个单位长度,得到点B,抛物线![]() 的顶点为C.
的顶点为C.
(1)求m的值和点B的坐标;
(2)求点C的坐标(用含n的代数式表示);
(3)若抛物线与线段AB只有一个公共点,结合函数图象,求n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
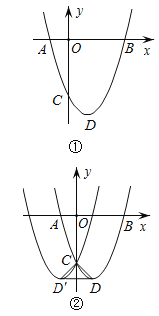
【题目】如图①,在平面直角坐标系中,抛物线![]() (
(![]() )与x轴相交于A,B两点,与y轴相交于点C,顶点为D.
)与x轴相交于A,B两点,与y轴相交于点C,顶点为D.
(1)当a=1时,抛物线顶点D的坐标为________,AB=_________;
(2)AB的长是否与a有关?说明你的理由;
(3)若将抛物线![]() (
(![]() )沿y轴折叠,得到另一抛物线,其顶点为D,如图②.连接CD,CD和DD.
)沿y轴折叠,得到另一抛物线,其顶点为D,如图②.连接CD,CD和DD.
①若△CDD为等边三角形时,则a=______;
②若△CDD为等腰直角三角形时,则a=______.
查看答案和解析>>
科目:初中数学 来源: 题型:
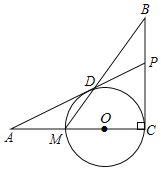
【题目】如图,已知BC⊥AC,圆心O在AC上,点M与点C分别是AC与⊙O的交点,点D是MB与⊙O的交点,点P是AD延长线与BC的交点,且ADAO=AMAP.
(1)连接OP,证明:△ADM∽△APO;
(2)证明:PD是⊙O的切线;
(3)若AD=12,AM=MC,求PB和DM的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】装商店销售![]() 台
台![]() 型和
型和![]() 台
台![]() 型电脑的利润为
型电脑的利润为![]() 元,销售
元,销售![]() 台
台![]() 型和
型和![]() 台,
台, ![]() 型电脑的利润为
型电脑的利润为![]() 元.
元.
(1)求每台![]() 型电脑和
型电脑和![]() 型电脑的销售利润;
型电脑的销售利润;
(2)该商店计划一次购进两种型号的电脑共 ![]() 台,其中
台,其中![]() 型电脑的进货量不超过
型电脑的进货量不超过![]() 型电脑的
型电脑的![]() 倍,购进
倍,购进![]() 型电脑
型电脑![]() 台,这
台,这![]() 台电脑的销售总利润为
台电脑的销售总利润为![]() 元.间该商店购进
元.间该商店购进![]() 型
型![]() 服各多少台.才能使销售利润
服各多少台.才能使销售利润![]() 最大?
最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,2×2网格(每个小正方形的边长为1)中有A,B,C,D,E,F,G,H,O九个格点.抛物线l的解析式为y=(-1)nx2+bx+c(n为整数).

(1)n为奇数,且l经过点H(0,1)和C(2,1),求b,c的值,并直接写出哪个格点是该抛物线上的顶点;
(2)n为偶数,且l经过点A(1, 0)和B(2,0),通过计算说明点F(0,2)和H(0,1)是否在抛物线上;
(3)若l经过这九个格点中的三个,直接写出满足这样条件的抛物线条数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com