
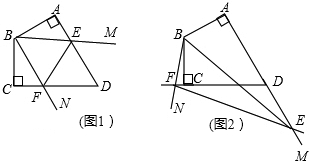
如图,∠MBN的两边BM,BN上分别有两点A、C,满足BC=2BA,作□ABCD,取AD的中点E,作CF⊥CD,CF与AB所在的直线交于点F。
(1)当∠B= 时,直接写出∠DEF的度数;
时,直接写出∠DEF的度数;
(2)在射线BM绕B点旋转的过程中,若∠B= ,∠DEF=
,∠DEF= (
( <X<
<X< ,
, <Y<
<Y< ),求:Y关于X的函数解析式及相应自变量X的取值范围,
),求:Y关于X的函数解析式及相应自变量X的取值范围, 
(1)∠DEF=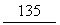 °;…………2分
°;…………2分
(2)对∠B的大小分三种情况讨论如下: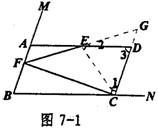
①当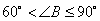 时,点F在线段AB上(见图7-1)。
时,点F在线段AB上(见图7-1)。
延长FE,并与CD的延长线交于点G,记∠AFE= 。
。
∵  ABCD,∴ AB∥CD,AD=BC,AB=CD,∠3=∠B=x°。
ABCD,∴ AB∥CD,AD=BC,AB=CD,∠3=∠B=x°。
∴∠DGE=∠AFE= 。
。
可得△AEF≌△DEG。
∴ EF=EG,CE为Rt△CFG斜边的中线。
∴ EF=EG,∠1=∠G= 。
。
∵ BC=2AB,
∴ 2DE=2CD,DE=CD。
∴等腰三角形△CDE中,∠1= 。
。
∴ 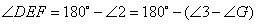
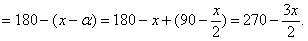 …………3分
…………3分
<1>当∠B=90°时,点F与点B重合,(见图7-2) 此时∠DEF=135°,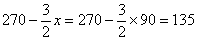 ,
,
所以 仍成立。…………4分
仍成立。…………4分
<2>当∠B=60°时,点F与点A重合,∠DEF=180°不合题意(见图7-3)。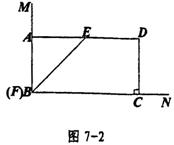
②当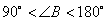 时,点F在线段AB的延长线上(见图7-4)。
时,点F在线段AB的延长线上(见图7-4)。
与①同理可得 。…………6分
。…………6分
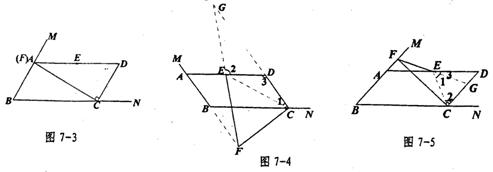
③当 时,点F在线段BA的延长线上(如图7-5)。
时,点F在线段BA的延长线上(如图7-5)。
与①同理可得CE为Rt△CFG斜边的中线,EC=EG,DE=CD。
∴△CEG和△CDE为等腰三角形。
在等腰三角形△CEG中,∠1=180°-2∠2,在等腰三角形△CDE中, ,
,
∴∠DEF=180°-∠3=180°-(∠CED-∠1)=360°-3∠2=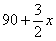 。…………7分
。…………7分
综上所述,当 时,
时,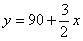 ;
;
当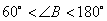 时,
时, 。
。
解析


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
 如图,∠MBN的两边BM,BN上分别有两点A、C,满足BC=2BA,作?ABCD,取AD的中点E,作CF⊥CD,CF与AB所在的直线交于点F.
如图,∠MBN的两边BM,BN上分别有两点A、C,满足BC=2BA,作?ABCD,取AD的中点E,作CF⊥CD,CF与AB所在的直线交于点F.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:2013届北京铁路第二中学初二期中数学试卷(解析版) 题型:解答题
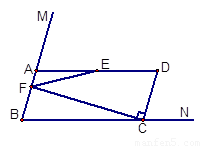
如图,∠MBN的两边BM,BN上分别有两点A、C,满足BC=2BA,作□ABCD,取AD的中点E,作CF⊥CD,CF与AB所在的直线交于点F。
(1)当∠B= 时,直接写出∠DEF的度数;
时,直接写出∠DEF的度数;
(2)在射线BM绕B点旋转的过程中,若∠B=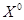 ,∠DEF=
,∠DEF=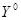 (
(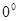 <X<
<X<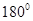 ,
,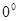 <Y<
<Y<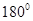 ),求:Y关于X的函数解析式及相应自变量X的取值范围,
),求:Y关于X的函数解析式及相应自变量X的取值范围,
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
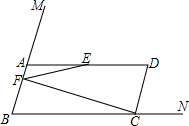 如图,∠MBN的两边BM,BN上分别有两点A、C,满足BC=2BA,作?ABCD,取AD的中点E,作CF⊥CD,CF与AB所在的直线交于点F.
如图,∠MBN的两边BM,BN上分别有两点A、C,满足BC=2BA,作?ABCD,取AD的中点E,作CF⊥CD,CF与AB所在的直线交于点F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com