
”¾ĢāÄæ”æČōÅ×ĪļĻßL£ŗy=ax2+bx+c£Øa£¬b£¬cŹĒ³£Źż£¬abc”Ł0£©ÓėÖ±Ļßl¶¼¾¹żyÖįÉĻµÄŅ»µćP£¬ĒŅÅ×ĪļĻßLµÄ¶„µćQŌŚÖ±ĻßlÉĻ£¬Ōņ³Ę“ĖÖ±ĻßlÓėøĆÅ×ĪļĻßL¾ßÓŠ”°Ņ»“ųŅ»Ā·”±¹ŲĻµ£®“ĖŹ±£¬Ö±Ļßl½Š×öÅ×ĪļĻßLµÄ”°“ųĻß”±£¬Å×ĪļĻßL½Š×öÖ±ĻßlµÄ”°Ā·Ļß”±£®
£Ø1£©ČōÖ±Ļßy=mx+1ÓėÅ×ĪļĻßy=x2©2x+n¾ßÓŠ”°Ņ»“ųŅ»Ā·”±¹ŲĻµ£¬Ēóm£¬nµÄÖµ£»
£Ø2£©Čōij”°Ā·Ļß”±LµÄ¶„µćŌŚ·“±ČĄżŗÆŹży=![]() µÄĶ¼ĻóÉĻ£¬ĖüµÄ”°“ųĻß”±lµÄ½āĪöŹ½ĪŖy=2x©4£¬Ēó“Ė”°Ā·Ļß”±LµÄ½āĪöŹ½£»
µÄĶ¼ĻóÉĻ£¬ĖüµÄ”°“ųĻß”±lµÄ½āĪöŹ½ĪŖy=2x©4£¬Ēó“Ė”°Ā·Ļß”±LµÄ½āĪöŹ½£»
£Ø3£©µ±³£ŹżkĀś×ć![]() ”Ük”Ü2Ź±£¬ĒóÅ×ĪļĻßL£ŗy=ax2+£Ø3k2©2k+1£©x+kµÄ”°“ųĻß”±lÓėxÖį£¬yÖįĖłĪ§³ÉµÄČż½ĒŠĪĆ껿µÄȔֵ·¶Ī§£®
”Ük”Ü2Ź±£¬ĒóÅ×ĪļĻßL£ŗy=ax2+£Ø3k2©2k+1£©x+kµÄ”°“ųĻß”±lÓėxÖį£¬yÖįĖłĪ§³ÉµÄČż½ĒŠĪĆ껿µÄȔֵ·¶Ī§£®
”¾“š°ø”æ£Ø1£©mµÄÖµĪŖ©1£¬nµÄÖµĪŖ1£®£Ø2£©y=2£Øx+1£©2©6»ņy=©![]() £Øx©3£©2+2£®£Ø3£©
£Øx©3£©2+2£®£Ø3£©![]() ”ÜS”Ü
”ÜS”Ü![]() £®
£®
”¾½āĪö”æ
ŹŌĢā·ÖĪö£ŗ£Ø1£©Č·¶ØÖ±Ļßy=mx+1ÓėyÖįµÄ½»µć×ų±ź£¬½«Ęä“śČėÅ×ĪļĻß½āĪöŹ½ÖŠ¼“æÉĒó³önµÄÖµ£»ŌŁøł¾ŻÅ×ĪļĻߵĽāĪöŹ½ÕŅ³ö¶„µć×ų±ź£¬½«Ęä“śČėÖ±Ļß½āĪöŹ½ÖŠ¼“æÉµĆ³ö½įĀŪ£»£Ø2£©Č·¶ØÖ±ĻßÓė·“±ČĄżŗÆŹżĶ¼ĻóµÄ½»µć×ų±ź£¬ÓÉ“ĖÉč³öÅ×ĪļĻߵĽāĪöŹ½£¬ŌŁÓÉÖ±ĻߵĽāĪöŹ½ÕŅ³öÖ±ĻßÓėxÖįµÄ½»µć×ų±ź£¬½«Ęä“śČėÅ×ĪļĻß½āĪöŹ½ÖŠ¼“æÉµĆ³ö½įĀŪ£»£Ø3£©ÓÉÅ×ĪļĻß½āĪöŹ½ÕŅ³öÅ×ĪļĻßÓėyÖįµÄ½»µć×ų±ź£¬ŌŁøł¾ŻÅ×ĪļĻߵĽāĪöŹ½ÕŅ³öĘ䶄µć×ų±ź£¬ÓÉĮ½µć×ų±ź½įŗĻ“ż¶ØĻµŹż·Ø¼“æÉµĆ³öÓėøĆÅ×ĪļĻ߶ŌÓ¦µÄ”°“ųĻß”±lµÄ½āĪöŹ½£¬ÕŅ³öøĆÖ±ĻßÓėx”¢yÖįµÄ½»µć×ų±ź£¬½įŗĻČż½ĒŠĪµÄĆ껿ÕŅ³öĆ껿S¹ŲÓŚkµÄ¹ŲĻµÉĻ£¬Óɶž“ĪŗÆŹżµÄŠŌÖŹ¼“æÉµĆ³ö½įĀŪ£®
ŹŌĢā½āĪö£ŗ£Ø1£©ĮīÖ±Ļßy=mx+1ÖŠx=0£¬Ōņy=1£¬
¼“Ö±ĻßÓėyÖįµÄ½»µćĪŖ£Ø0£¬1£©£»
½«£Ø0£¬1£©“śČėÅ×ĪļĻßy=x2©2x+nÖŠ£¬
µĆn=1£®
”ßÅ×ĪļĻߵĽāĪöŹ½ĪŖy=x2©2x+1=£Øx©1£©2£¬
”ąÅ×ĪļĻߵĶ„µć×ų±źĪŖ£Ø1£¬0£©£®
½«µć£Ø1£¬0£©“śČėµ½Ö±Ļßy=mx+1ÖŠ£¬
µĆ£ŗ0=m+1£¬½āµĆ£ŗm=©1£®
“š£ŗmµÄÖµĪŖ©1£¬nµÄÖµĪŖ1£®
£Ø2£©½«y=2x©4“śČėµ½y=![]() ÖŠÓŠ£¬
ÖŠÓŠ£¬
2x©4=![]() £¬¼“2x2©4x©6=0£¬
£¬¼“2x2©4x©6=0£¬
½āµĆ£ŗx1=©1£¬x2=3£®
”ąøĆ”°Ā·Ļß”±LµÄ¶„µć×ų±źĪŖ£Ø©1£¬©6£©»ņ£Ø3£¬2£©£®
Įī”°“ųĻß”±l£ŗy=2x©4ÖŠx=0£¬Ōņy=©4£¬
”ą”°Ā·Ļß”±LµÄĶ¼Ļó¹żµć£Ø0£¬©4£©£®
ÉčøĆ”°Ā·Ļß”±LµÄ½āĪöŹ½ĪŖy=m£Øx+1£©2©6»ņy=n£Øx©3£©2+2£¬
ÓÉĢāŅāµĆ£ŗ©4=m£Ø0+1£©2©6»ņ©4=n£Ø0©3£©2+2£¬
½āµĆ£ŗm=2£¬n=©![]() £®
£®
”ą“Ė”°Ā·Ļß”±LµÄ½āĪöŹ½ĪŖy=2£Øx+1£©2©6»ņy=©![]() £Øx©3£©2+2£®
£Øx©3£©2+2£®
£Ø3£©ĮīÅ×ĪļĻßL£ŗy=ax2+£Ø3k2©2k+1£©x+kÖŠx=0£¬Ōņy=k£¬
¼“øĆÅ×ĪļĻßÓėyÖįµÄ½»µćĪŖ£Ø0£¬k£©£®
Å×ĪļĻßL£ŗy=ax2+£Ø3k2©2k+1£©x+kµÄ¶„µć×ų±źĪŖ£Ø©![]() £¬
£¬![]() £©£¬
£©£¬
Éč”°“ųĻß”±lµÄ½āĪöŹ½ĪŖy=px+k£¬
”ßµć£Ø©![]() £¬
£¬![]() £©ŌŚy=px+kÉĻ£¬
£©ŌŚy=px+kÉĻ£¬
”ą![]() =©p
=©p![]() +k£¬
+k£¬
½āµĆ£ŗp=![]() £®
£®
”ą”°“ųĻß”±lµÄ½āĪöŹ½ĪŖy=![]() x+k£®
x+k£®
Įī”ą”°“ųĻß”±l£ŗy=![]() x+kÖŠy=0£¬Ōņ0=
x+kÖŠy=0£¬Ōņ0=![]() x+k£¬
x+k£¬
½āµĆ£ŗx=©![]() £®
£®
¼“”°“ųĻß”±lÓėxÖįµÄ½»µćĪŖ£Ø©![]() £¬0£©£¬ÓėyÖįµÄ½»µćĪŖ£Ø0£¬k£©£®
£¬0£©£¬ÓėyÖįµÄ½»µćĪŖ£Ø0£¬k£©£®
”ą”°“ųĻß”±lÓėxÖį£¬yÖįĖłĪ§³ÉµÄČż½ĒŠĪĆ껿S=![]() |©
|©![]() |”Į|k|£¬
|”Į|k|£¬
”ß![]() ”Ük”Ü2£¬
”Ük”Ü2£¬
”ą![]() ”Ü
”Ü![]() ”Ü2£¬
”Ü2£¬
”ąS=![]() =
=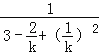 =
=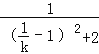 £¬
£¬
µ±![]() =1Ź±£¬SÓŠ×ī“óÖµ£¬×ī“óÖµĪŖ
=1Ź±£¬SÓŠ×ī“óÖµ£¬×ī“óÖµĪŖ![]() £»
£»
µ±![]() =2Ź±£¬SÓŠ×īŠ”Öµ£¬×īŠ”ÖµĪŖ
=2Ź±£¬SÓŠ×īŠ”Öµ£¬×īŠ”ÖµĪŖ![]() £®
£®
¹ŹÅ×ĪļĻßL£ŗy=ax2+£Ø3k2©2k+1£©x+kµÄ”°“ųĻß”±lÓėxÖį£¬yÖįĖłĪ§³ÉµÄČż½ĒŠĪĆ껿µÄȔֵ·¶Ī§ĪŖ![]() ”ÜS”Ü
”ÜS”Ü![]() £®
£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”潫ĻĀĮŠ¶ąĻīŹ½·Ö½āŅņŹ½£¬½į¹ūÖŠ²»ŗ¬ŅņŹ½x©1µÄŹĒ£Ø””””£©
A. x2©1 B. x£Øx©2£©+£Ø2©x£© C. x2©2x+1 D. x2+2x+1
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æµćµ½Ö±ĻߵľąĄėŹĒÖøÕāµćµ½ÕāĢõÖ±ĻßµÄ
A”¢“¹Ļ߶ĪB”¢“¹Ļߵij¤
C”¢³¤¶ČD”¢“¹Ļ߶ĪµÄ³¤¶Č
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ(1)ČēĶ¼ a£¬Čō AB”ĪCD£¬µć P ŌŚ AB”¢CD Ķā²æ£¬Ōņ”ĻBPD”¢”ĻB”¢”ĻD Ö®¼äÓŠŗĪŹżĮæ¹ŲĻµ£æ
°ŃĻĀĆęµÄ½ā“šĢīÉĻøł¾Ż£ŗ
½ā£ŗ”ĻB=”ĻBPD+”ĻPDC£®
ĄķÓÉ£ŗ×÷PE”ĪAB
”ß AB”ĪCD ( )
”ąAB”ĪCD”ĪPE ( )
”ą”ĻB=”ĻBPE£¬ ”ĻD=”ĻDPE ( )
”ß”ĻBPE=”ĻBPD+”ĻDPE
”ą”ĻB=”ĻBPD+”ĻPDC ( )
(2)ČōAB”ĪCD£¬½«µćPŅʵ½AB”¢CDÄŚ²æ£¬ČēĶ¼b£¬ŅŌÉĻ½įĀŪŹĒ·ń³ÉĮ¢£æČō³ÉĮ¢£¬ĖµĆ÷ĄķÓÉ£»Čō²»³ÉĮ¢£¬Ōņ”ĻBPD”¢”ĻB”¢”ĻD Ö®¼äÓŠŗĪŹżĮæ¹ŲĻµ£æĒėÖ¤Ć÷ÄćµÄ½įĀŪ.
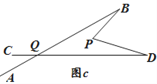
(3)ŌŚĶ¼ b ÖŠ£¬½«Ö±Ļß AB ČʵćBÄꏱÕė·½ĻņŠż×ŖŅ»¶Ø½Ē¶Č½»Ö±Ļß CD ÓŚµć Q£¬ČēĶ¼ c£¬Ōņ”ĻBPD”¢”ĻB”¢”ĻD”¢”ĻBQD Ö®¼äĀś×ćµÄŹżĮæ¹ŲĻµŹĒ .
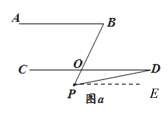
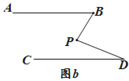
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĻĀĮŠĖµ·ØÕżČ·µÄŹĒ(””””)
A. ÕżÕūŹżŗĶøŗÕūŹżĶ³³ĘÕūŹż
B. ÓŠĄķŹż·ÖĪŖÕżÓŠĄķŹżŗĶøŗÓŠĄķŹż
C. ÓŠĄķŹżŹĒÖøÕūŹż£¬·ÖŹż£¬ÕżÓŠĄķŹż£¬øŗÓŠĄķŹżŗĶĮćÕāĪåĄąŹż
D. ÕūŹżŗĶ·ÖŹżĶ³³ĘÓŠĄķŹż
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ¼ĘĖć6a6”Ā3a2µÄ½į¹ūĪŖ£Ø””””£©
A. 3a4B. 3a3C. 2a3D. 2a4
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĶ¬Ņ»Ę½ĆęÄŚÓŠĖÄĢõÖ±Ļßa”¢b”¢c”¢d£¬Čōa”Īb£¬a”Ķc£¬b”Ķd£¬ŌņÖ±Ļßc”¢dµÄĪ»ÖĆ¹ŲĻµĪŖ£Ø £©
A. »„Ļą“¹Ö± B. »„ĻąĘ½ŠŠ C. Ļą½» D. ĪŽ·ØČ·¶Ø
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ”ŃOµÄ°ė¾¶ĪŖ7cm£¬µćPµ½Ō²ŠÄOµÄ¾ąĄėOP=10cm£¬ŌņµćPÓė”ŃOµÄĪ»ÖĆ¹ŲĻµĪŖ£Ø”” ””£©
A. µćPŌŚŌ²ÉĻ B. µćPŌŚŌ²ÄŚ C. µćPŌŚŌ²Ķā D. ĪŽ·ØČ·¶Ø
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌ²×¶µ×ĆęŌ²µÄ°ė¾¶ĪŖ2£¬ÄøĻß³¤ĪŖ5£¬ĖüµÄ²ąĆ껿µČÓŚ_____£Ø½į¹ū±£Įō¦Š£©£®
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com