【题目】已知四边形ABCD中，AB//CD，AC//BD，下列判断中正确的是 ( )
A. 如果BC=AD，那么四边形ABCD是等腰梯形；
B. 如果AD//BC，那么四边形ABCD是菱形；
C. 如果AC平分BD，那么四边形ABCD是矩形；
D. 如果AC⊥BD，那么四边形ABCD是正方形.
科目：初中数学 来源： 题型：
【题目】已知：如图1，四边形ABCD是平行四边形，E,F是对角线AC上的两点，AE=CF.
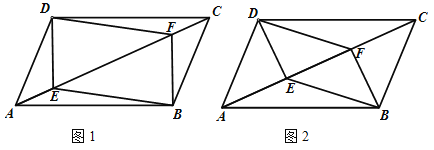
（1）求证：四边形DEBF是平行四边形；
（2）如果AE=EF=FC,请直接写出图中2所有面积等于四边形DEBF的面积的三角形.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】我国古代对于利用方程解决实际问题早有研究，《九章算术》中提到这么一道“以绳测井”的题：以绳测井，若将绳三折测之，绳多四尺：若将绳四折测之，绳多一尺．绳长、井深各几何？
这道题大致意思是：用绳子测量水井深度，如果将绳子折成三等份，那么每等份井外余绳四尺：如果将绳子折成四等份，那么每等份井外余绳一尺．问绳长和井深各多少尺？若设井深为x尺，则求解井深的方程正确的是（ ）
A.3（x+4）＝4（x+1）B.3x+4＝4x+1
C.
x+4＝
x+1D.x﹣4＝x﹣1
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为了了解2014年某地区10万名大、中、小学生50米跑成绩情况，教育部门从这三类学生群体中各抽取了10%的学生进行检测，整理样本数据，并结合2010年抽样结果，得到下列统计图：
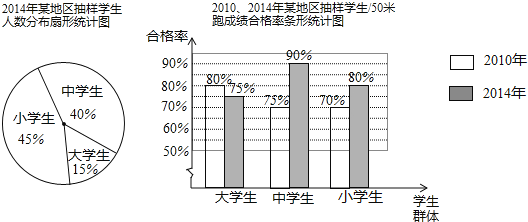
（1）本次检测抽取了大、中、小学生共 名，其中小学生 名；
（2）根据抽样的结果，估计2014年该地区10万名大、中、小学生中，50米跑成绩合格的中学生人数为 名；
（3）比较2010年与2014年抽样学生50米跑成绩合格率情况，写出一条正确的结论．
查看答案和解析>>
科目：初中数学 来源： 题型：
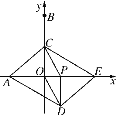
【题目】如图，在平面直角坐标系中，点A，B的坐标分别是(－3，0)，(0，6)，动点P从点O出发，沿x轴正方向以每秒1个单位的速度运动，同时动点C从点B出发，沿射线BO方向以每秒2个单位的速度运动．以CP，CO为邻边构造PCOD.在线段OP延长线上一动点E，且满足PE＝AO.
(1)当点C在线段OB上运动时，求证：四边形ADEC为平行四边形；
(2)当点P运动的时间为
秒时，求此时四边形ADEC的周长是多少．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如果抛物线C: y=ax2+bx+c（a≠0）与直线l：y=kx+d（k≠0）都经过y轴上一点P，且抛物线C的顶点Q在直线l上，那么称此直线l与该抛物线C具有“一带一路”关系．如果直线y=mx+1与抛物线y=x2-2x+n具有“一带一路”关系，那么m+n=_________．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在等腰直角三角形ACD，∠ACD=90°，AC=
，分别以边AD，AC，CD为直径面半图，所得两个月形图案AGCE和DHCF的面积之和(图中阴影部分)为_____________。
查看答案和解析>>
科目：初中数学 来源： 题型：
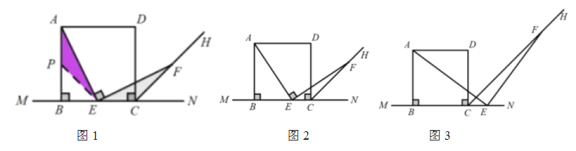
【题目】如图1，以直线MN上的线段BC为边作正方形ABCD，CH平分∠DCN，点E为射线BN上一点，连接AE，过点E作AE的垂线交射线CH于点F，探索AE与EF的数量关系。
(1)阅读下面的解答过程。并按此思路完成余下的证明过程
当点E在线段BC上，且点E为BC中点时，AB=EF
理由如下：
取AB中点P，達接PE
在正方形ABCD中，∠B=∠BCD=90°，AB=BC
∴△BPE等腰三角形，AP=BC
∴∠BPB=45°
∴∠APBE=135°
又因为CH平分∠DCN
∴∠DCF=45°
∴∠ECF=135°
∴∠APE=∠ECF
余下正明过程是：
(2)当点E为线段AB上任意一点时，如图2，结论“AE=EF”是否成立，如果成立，请给出证明过程；
(3)当点E在BC的延长线时，如图3，结论“AE=EF”是否仍然成立，如果成立，请在图3中画出必要的辅助线(不必说明理由)。
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，将n个边长都为2的正方形按如图所示摆放，点A1，A2，…An分别是正方形的中心，则这n个正方形重叠部分的面积之和是（ ）
A.nB.n﹣1C.
D.
n
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
