
【题目】已知关于x的方程x2﹣(m+2)x+(2m﹣1)=0.
(1)求证:方程恒有两个不相等的实数根;
(2)若此方程的一个根是1,请求出方程的另一个根,并求以此两根为边长的直角三角形的周长.
【答案】
(1)证明:∵△=(m+2)2﹣4(2m﹣1)=(m﹣2)2+4,
∴在实数范围内,m无论取何值,(m﹣2)2+4>0,即△>0,
∴关于x的方程x2﹣(m+2)x+(2m﹣1)=0恒有两个不相等的实数根
(2)解:根据题意,得
12﹣1×(m+2)+(2m﹣1)=0,
解得,m=2,
则方程的另一根为:m+2﹣1=2+1=3;
①当该直角三角形的两直角边是1、3时,由勾股定理得斜边的长度为: ![]() ;
;
该直角三角形的周长为1+3+ ![]() =4+
=4+ ![]() ;
;
②当该直角三角形的直角边和斜边分别是1、3时,由勾股定理得该直角三角形的另一直角边为2 ![]() ;则该直角三角形的周长为1+3+2
;则该直角三角形的周长为1+3+2 ![]() =4+2
=4+2 ![]()
【解析】(1)根据关于x的方程x2﹣(m+2)x+(2m﹣1)=0的根的判别式的符号来证明结论;(2)根据一元二次方程的解的定义求得m值,然后由根与系数的关系求得方程的另一根.分类讨论:①当该直角三角形的两直角边是2、3时,由勾股定理得斜边的长度为: ![]() ;②当该直角三角形的直角边和斜边分别是2、3时,由勾股定理得该直角三角形的另一直角边为
;②当该直角三角形的直角边和斜边分别是2、3时,由勾股定理得该直角三角形的另一直角边为 ![]() ;再根据三角形的周长公式进行计算.
;再根据三角形的周长公式进行计算.
【考点精析】关于本题考查的求根公式和勾股定理的概念,需要了解根的判别式△=b2-4ac,这里可以分为3种情况:1、当△>0时,一元二次方程有2个不相等的实数根2、当△=0时,一元二次方程有2个相同的实数根3、当△<0时,一元二次方程没有实数根;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能得出正确答案.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,已知AB=AC=5,BC=6,且△ABC≌△DEF,将△DEF与△ABC重合在一起,△ABC不动,△DEF运动,并满足:点E在边BC上沿B到C的方向运动,且DE、始终经过点A,EF与AC交于M点. 
(1)求证:△ABE∽△ECM;
(2)探究:在△DEF运动过程中,重叠部分能否构成等腰三角形?若能,求出BE的长;若不能,请说明理由;
(3)当线段AM最短时,求重叠部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
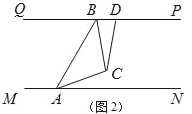
【题目】“一带一路”让中国和世界更紧密,“中欧铁路”为了安全起见在某段铁路两旁安置了两座可旋转探照灯.如图1所示,灯A射线从AM开始顺时针旋转至AN便立即回转,灯B射线从BP开始顺时针旋转至BQ便立即回转,两灯不停交叉照射巡视.若灯A转动的速度是每秒2度,灯B转动的速度是每秒1度.假定主道路是平行的,即PQ∥MN,且∠BAM:∠BAN=2:1.
(1)填空:∠BAN=_____°;
(2)若灯B射线先转动30秒,灯A射线才开始转动,在灯B射线到达BQ之前,A灯转动几秒,两灯的光束互相平行?
(3)如图2,若两灯同时转动,在灯A射线到达AN之前.若射出的光束交于点C,过C作∠ACD交PQ于点D,且∠ACD=120°,则在转动过程中,请探究∠BAC与∠BCD的数量关系是否发生变化?若不变,请求出其数量关系;若改变,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂用如图甲所示的长方形和正方形纸板,做成如图乙所示的竖式与横式两种长方体形状的无盖纸盒.

(1)现有正方形纸板162张,长方形纸板340张.若要做两种纸盒共100个,设做竖式纸盒x个.
①根据题意,完成以下表格:
纸盒 纸板 | 竖式纸盒(个) | 横式纸盒(个) |
x | 100﹣x | |
正方形纸板(张) | 2(100﹣x) | |
长方形纸板(张) | 4x |
②按两种纸盒的生产个数来分,有哪几种生产方案?
(2)若有正方形纸162张,长方形纸板a张,做成上述两种纸盒,纸板恰好用完.已知290<a<306.求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有以下说法:其中正确的说法有( )
(1)开方开不尽的数是无理数;
(2)无理数是无限循环小数
(3)无理数包括正无理数和负无理数;
(4)无理数都可以用数轴上的点来表示;
(5)循环小数都是有理数
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,弦CD⊥AB于H,过CD延长线上一点E作⊙O的切线交AB的延长线于F.切点为G,连接AG交CD于K. 
(1)求证:KE=GE;
(2)若KG2=KDGE,试判断AC与EF的位置关系,并说明理由;
(3)在(2)的条件下,若sinE= ![]() ,AK=2
,AK=2 ![]() ,求FG的长.
,求FG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
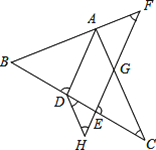
【题目】如图,AD平分∠BAC交BC于点D,点F在BA的延长线上,点E在线段CD上,EF与AC相交于点G,∠BDA+∠CEG=180°.
(1)AD与EF平行吗?请说明理由;
(2)若点H在FE的延长线上,且∠EDH=∠C,则∠F与∠H相等吗,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com