在直角坐标系中,点A,B,C,D的坐标依次是(1,0),(a,b),(1,6),(m,n),要使四边形ABCD为菱形(A,B,C,D按逆时针排列),且面积为24,求B,D两点的坐标.
分析:由点A,C的坐标知点A、C在平行于y轴的直线x=1上,根据菱形的性质:对角线相互垂直且平分,来求点E的坐标为(1,3)及B、D、应该在平行于x轴的直线上;然后根据菱形的面积公式S
菱形ABCD=
BD•AC及两点间的距离公式求得
BD=8;最后根据两点间的距离公式求得DE=BE=4,即|m-1|=|a-1|=
|m-a|=4,所以m=5,a=-3,从而求得B、D两点的坐标.
解答: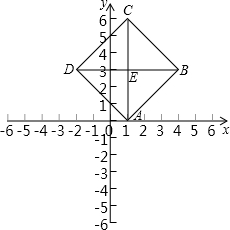
解:∵四边形ABCD为菱形,
∴对角线AC⊥BD,且CE=AE;
∵A,C的坐标依次是(1,0),(1,6),
∴A、C在平行于y轴的直线x=1上,且E(1,3)
∴B、D、E应该在平行于x轴的直线上;
∵B,D的坐标依次是(a,b),(m,n),
∴b=n=3;
又∵菱形ABCD的面积是24,
∴S
菱形ABCD=
BD•AC=
|m-a|•(6-0)=24,即|m-a|=8;
又∵DE=BE,
∴|m-1|=|a-1|=
|m-a|=4;
又∵A,B,C,D按逆时针排列(如图所示),
∴m=5,a=-3,
∴B(5,3)、D(-3,3).
点评:本题考查了是菱形的性质、点的坐标与图形性质.解题时,采用了“数形结合”的数学思想,通过菱形的对角线互相垂直平分及两点间的距离公式来求得B、D两点的坐标.

 解:∵四边形ABCD为菱形,
解:∵四边形ABCD为菱形,

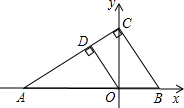 C作CB⊥AC,交x轴于B.
C作CB⊥AC,交x轴于B.