
【题目】为配合全市“禁止焚烧秸秆”工作,某学校举行了“禁止焚烧秸秆,保护环境,从我做起”为主题的演讲比赛. 赛后组委会整理参赛同学的成绩,并制作了如下不完整的频数分布表和频数分布直方图,请根据图表提供的信息,解答下列问题:
分数段 (分数为x分) | 频数 | 百分比 |
60≤x<70 | 8 | 20% |
70≤x<80 | a | 30% |
80≤x<90 | 16 | b% |
90≤x<100 | 4 | 10% |
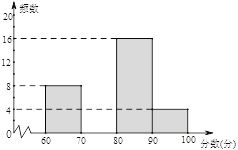
(1)表中的a= ,b= ;
(2)请补全频数分布直方图;
(3)若用扇形统计图来描述成绩分布情况,则分数段70≤x<80对应的圆心角的度数是 ;
(4)竞赛成绩不低于90分的4名同学中正好有2名男同学,2名女同学.学校从这4名同学中随机抽取2名同学接受电视台记者采访,请用列表或画树状图的方法求正好抽到一名男同学和一名女同学的概率.
【答案】(1)a=12,b=40;(2)详见解析;(3)108°;(4)![]() .
.
【解析】
(1)首先根据第一小组的频数和频率求得总人数,然后减去其它小组的频数即可求得a值,根据总人数和第三小组的频数即可求得b值;
(2)根据(1)求出的a的值,可直接补图;
(3)用周角乘以相应分数段所占的百分比即可求得圆心角的度数;
(4)列表将所有等可能的结果列举出来,利用概率公式求解即可.
(1)∵60≤x<70小组的频数为8,占20%,
∴8÷20%=40人,
∴a=40-8-16-4=12,
b%=![]() ×100%=40%,即b=40;
×100%=40%,即b=40;
故答案为:12,40;
(2)根据(1)求出a=12,补图如下: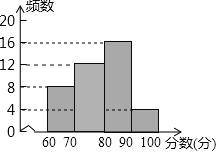
(3)∵70≤x<80小组所占的百分比为30%,
∴70≤x<80对应扇形的圆心角的度数360°×30%=108°,
故答案为:108°;
(4)用A、B表示男生,用a、b表示女生,列表得:
A | B | a | b | |
A | AB | Aa | Ab | |
B | BA | Ba | Bb | |
a | aA | aB | ab | |
b | bA | bB | ba |
∵共有12种等可能的结果,其中一男一女的有8种情况,
∴P(一男一女)= ![]() .
.


科目:初中数学 来源: 题型:
【题目】雾霾是对大气中各种悬浮颗粒物含量超标的笼统表述,雾霾的主要危害可归纳为两种:一是对人体产生危害,二是对交通产生危害.雾霾天气是一种大气污染状态,成都市区冬天雾霾天气比较严重,很多家庭兴起了为家里添置“空气清洁器”的热潮,为此,我市某商场根据民众健康要,代理销售某种进价为600元/台的家用“空气清洁器”.经过市场销售后发现:在一个月内,当售价是700元/台时,可售出350台,且售价每提高10元,就会少售出5台.
(1)试确定月销售量y(台)与售价x(元/台)之间的函数关系式;
(2)请计算当售价x(元台)定为多少时,该商场每月销售这种“空气清洁器”所获得的利润W(元)最大?最大利润是多少?
(3)若政府计划遴选部分商场,将销售“空气清洁器”纳入民生工程项目,规定:每销售一台“空气淸洁器”,财政补贴商家200元,但销售利润不能高于进价的25%,请问:该商场想获取最大利润,是否参与竞标此民生工程项目?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在春季“植树节”活动中,王亮和李明两位同学想通过摸球的方式来决定谁去参加学校的植树节活动,规则如下:在两个盒子内分别装入标有数字1,2,3,4的四个和标有数字1,2,3的三个完全相同的小球,分别从两个盒子中摸出一个小球,如果所摸出的小球上的数字之和小于6,那么王亮去,否则就是李明去.
(1)用画树状图或列表的方法,求出王亮去的概率;
(2)李明说:“这种规则不公平”,你认同他的说法吗?请你说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A(3,1),B(1,0),PQ是直线y=x上的一条动线段且PQ=![]() (Q在P的下方),当AP+PQ+QB取最小值时,点Q坐标为______.
(Q在P的下方),当AP+PQ+QB取最小值时,点Q坐标为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系xOy中,抛物线C:y=ax2+bx+c与x轴相交于A,B两点,顶点为D(0,4),AB=4![]() ,设点F(m,0)是x轴的正半轴上一点,将抛物线C绕点F旋转180°,得到新的抛物线C/.
,设点F(m,0)是x轴的正半轴上一点,将抛物线C绕点F旋转180°,得到新的抛物线C/.
(1)求抛物线C的函数表达式;
(2)若抛物线C/与抛物线C在y轴的右侧有两个不同的公共点,求m的取值范围.
(3)如图2,P是第一象限内抛物线C上一点,它到两坐标轴的距离相等,点P在抛物线C/上的对应点P/,设M是C上的动点,N是C/上的动点,试探究四边形PMP/N能否成为正方形?若能,请直接写出m的值;若不能,请说明理由.
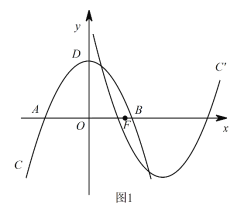

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:给定一个矩形,如果存在另一个矩形,它的周长和面积分别是已知矩形的周长和面积的2倍,则这个矩形是给定矩形的“加倍”矩形.如图,矩形![]() 是矩形
是矩形![]() 的“加倍”矩形.
的“加倍”矩形.
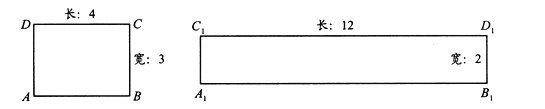
解决问题:
(1)当矩形的长和宽分别为3,2时,它是否存在“加倍”矩形?若存在,求出“加倍”矩形的长与宽,若不存在,请说明理由.
(2)边长为![]() 的正方形存在“加倍”正方形吗?请做出判断,并说明理由.
的正方形存在“加倍”正方形吗?请做出判断,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学习小组做“用频率估计概率的试验时,统计了某一结果出现的频率,绘制了如图所示折线统计图,则符合这一结果的试验最有可能的是( )
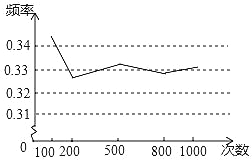
A. 掷一枚正六面体的骰子,出现1点朝上
B. 任意写一个整数,它能被2整除
C. 不透明袋中装有大小和质地都相同的1个红球和2个黄球,从中随机取一个,取到红球
D. 先后两次掷一枚质地均匀的硬币,两次都出现反面
查看答案和解析>>
科目:初中数学 来源: 题型:
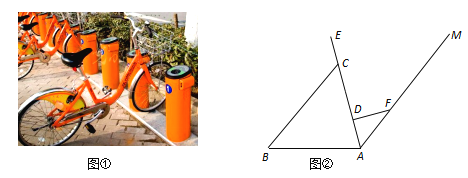
【题目】“低碳环保,你我同行”.近几年,各大城市的公共自行车给市民出行带来了极大的方便.图①是公共自行车的实物图,图②是公共自行车的车架示意图,点A.D、C、E在同一条直线上,CD=30cm,DF=20cm,AF=25cm,FD⊥AE于点D,座杆CE=15cm,且∠EAB=75°.
(1)求AD的长;
(2)求点E到AB的距离.(参考数据:sin75°≈0.97,cos75°≈0.26,tan75°≈3.73)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com