
 与抛物线
与抛物线 交于A、B两点,点A在x轴上,点B的横坐标为-8.
交于A、B两点,点A在x轴上,点B的横坐标为-8.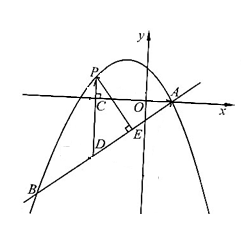
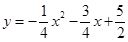 ;
;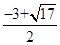 ,2),P2(
,2),P2(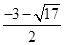 ,2),P3(
,2),P3(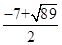 ,
,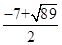 ).
).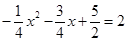 ,解得
,解得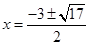 ,
,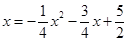 ,解得
,解得 ,可得P点坐标.
,可得P点坐标. ,当y=0,x=2.当x=﹣8时,y=﹣
,当y=0,x=2.当x=﹣8时,y=﹣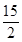 .
.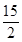 ).
). 经过A、B两点,
经过A、B两点,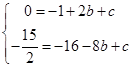
 .
.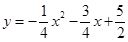 ;
; 与y轴交于点M,
与y轴交于点M,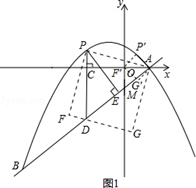
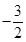 .∴OM=
.∴OM=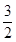 .
.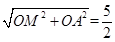 .
.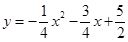 ﹣(
﹣(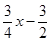 )=﹣
)=﹣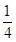 x2﹣
x2﹣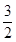 x+4,
x+4,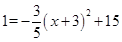 .
.
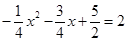 ,解得
,解得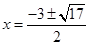 ,
,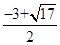 ,2),P2(
,2),P2(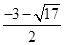 ,2),
,2),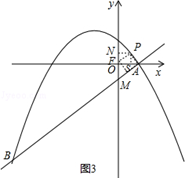
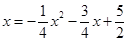 ,解得
,解得 ,
,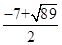 ,
,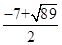 ),P4(
),P4( ,
, ),(舍去).
),(舍去).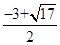 ,2),P2(
,2),P2(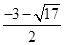 ,2),P3(
,2),P3(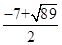 ,
,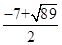 ).
).

 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案科目:初中数学 来源:不详 题型:解答题
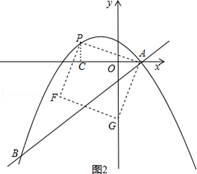
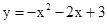 的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.
的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点. DQ,求点F的坐标.
DQ,求点F的坐标.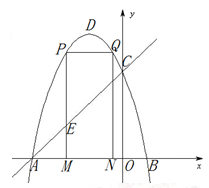
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 经过A(-1,0),C(3,-2)两点,与
经过A(-1,0),C(3,-2)两点,与 轴交于点D,与
轴交于点D,与 轴交于另一点B.
轴交于另一点B.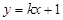 (
( )将四边形ABCD面积二等分,求
)将四边形ABCD面积二等分,求 的值;
的值; 轴于点F,将△AEF绕平面内某点P旋转180°得△MNQ(点M、N、Q分别与点A、E、F对应),使点M、N在抛物线上,求点N和点P的坐标?
轴于点F,将△AEF绕平面内某点P旋转180°得△MNQ(点M、N、Q分别与点A、E、F对应),使点M、N在抛物线上,求点N和点P的坐标?
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.b≥-1 | B.b≤-1 | C.b≥1 | D.b≤1 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题

 C.2
C.2 D.2
D.2 +2
+2查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 可以由抛物线
可以由抛物线 平移得到,则下列平移过程正确的是
平移得到,则下列平移过程正确的是| A.先向左平移2个单位,再向上平移3个单位 |
| B.先向左平移2个单位,再向下平移3个位 |
| C.先向右平移2个单位,再向下平移3个单位 |
| D.先向右平移2个单位,再向上平移3个单位 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题

A. | B. | C. | D. |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
|
二次函数 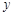 = =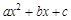 ( (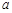 ≠0)图象如图所示,下列结论:① ≠0)图象如图所示,下列结论:①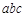 >0;② >0;② =0;③当 =0;③当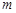 ≠1时, ≠1时, > > ;④ ;④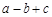 >0;⑤若 >0;⑤若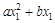 = = ,且 ,且 ≠ ≠ ,则 ,则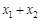 =2.其中正确的有( ) =2.其中正确的有( )
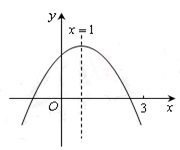 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题

 B.
B.
 D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com