
如图9,等腰梯形ABCD中,AD∥BC,点E是线段AD上的一个动点(E与A、D不重合),G、F、H分别是BE、BC、CE的中点.
(1)试探索四边形EGFH的形状,并说明理由;
(2)当点E运动到什么位置时,四边形EGFH是菱形?并加以证明;
(3)若(2)中的菱形EGFH是正方形,请探索线段EF与线段BC的关系,并证明你的结论.
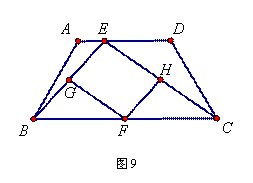
解(1)四边形EGFH是平行四边形
证明:∵G、F、H分别是BE、BC、CE的中点,
∴GF∥EH,GF=EH
∴四边形EGFH是平行四边形
(2)当点E是AD的中点时,四边形EGFH是菱形
证明:∵四边形ABCD是等腰梯形,
∴AB=CD,∠A=∠D
∵AE=DE
∴△ABE≌△DCE
∴BE=CE
∵G、H分别是BE、CE的中点
∴EG=EH
又由(1)知四边形EGFH是平行四边形
∴四边形EGFH是菱形
(3)EF⊥BC,EF=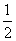 BC
BC
证明:∵四边形EGFH是正方形
∴EG=EH, ∠BEC=90°
∵G、H分别是BE、CE的中点
∴EB=EC
∵F是BC的中点
∴EF⊥BC,EF=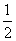 BC
BC
用其它证明方法也得分,过程略。


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:
(1)如图14,矩形ABCD中,AB=5cm,BC=2cm,在AB边上取一点E,(点E与A、B 不重合),连接DE、CE,分矩形ABCD所成的3个三角形都相似.我们把这样的点E叫做矩形ABCD的AB边上的强相似点,在图12的AB边上画出满足要求的强相似点E,并求
不重合),连接DE、CE,分矩形ABCD所成的3个三角形都相似.我们把这样的点E叫做矩形ABCD的AB边上的强相似点,在图12的AB边上画出满足要求的强相似点E,并求 AE的长;(画图工具不限)
AE的长;(画图工具不限)
 |
(2)对于任意一个矩形ABCD,AB边上是否一定存在这样的强相似点E?如果一定存在,请说明理由;如果不一定存在,请举例说明;
(3)在四边形ABCD中,AD∥BC,AD<BC,∠B=90°,当点E是四边形ABCD的AB边上的一个强相似点时.
猜想:AE与BE的数量关系__________________________.
并分别给出理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图1,一次函数与反比例函数的图象相交于A、B两点,则图中使反比例函数的值小于一次函数的值的x的取值范围是( )
A. x<-1 B. x>2
| |
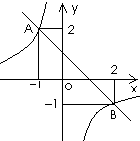
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,已知AB=DC,AD=BC,E,F在DB上两点且BF=DE,若∠AEB=120°,
∠ADB=30°,则∠BCF= ( )[
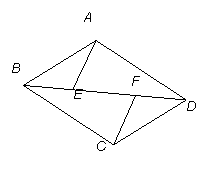 A.150° B.40° C.80° D.90°
A.150° B.40° C.80° D.90°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com