
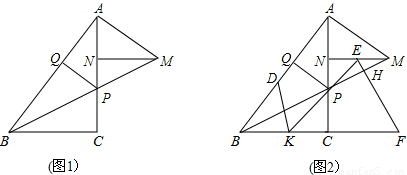
已知:在△ABC中,∠ACB=900,点P是线段AC上一点,过点A作AB的垂线,交BP的延长线于点M,MN⊥AC于点N,PQ⊥AB于点Q,A0=MN.
(1)如图l,求证:PC=AN;
(2) 如图2,点E是MN上一点,连接EP并延长交BC于点K,点D是AB上一点,连接DK,∠DKE=∠ABC,EF⊥PM于点H,交BC延长线于点F,若NP=2,PC=3,CK:CF=2:3,求DQ的长.
(1)证明见解析(2)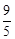
【解析】解:(1)证明:∵BA⊥AM,MN⊥AP,∴∠BAM=ANM=90°。
∴∠PAQ+∠MAN=∠MAN+∠AMN=90°,∴∠PAQ=∠AMN。
∵PQ⊥AB MN⊥AC,∴∠PQA=∠ANM=90°。∴AQ=MN。∴△AQP≌△MNA(ASA)。
∴AN=PQ,AM=AP。∴∠AMB=∠APM。
∵∠APM=∠BPC∠BPC+∠PBC=90°,∠AMB+∠ABM=90°,∴∠ABM=∠PBC。
∵PQ⊥AB,PC⊥BC,∴PQ=PC(角平分线的性质)。∴PC=AN。
(2)∵NP=2 PC=3,∴由(1)知PC=AN=3。∴AP=NC=5,AC=8。
∴AM=AP=5。∴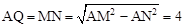 。
。
∵∠PAQ=∠AMN,∠ACB=∠ANM=90°,∴∠ABC=∠MAN。
∴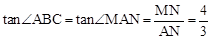 。
。
∵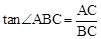 ,∴BC=6。
,∴BC=6。
∵NE∥KC,∴∠PEN=∠PKC。
又∵∠ENP=∠KCP,∴△PNE∽△PCK。∴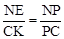 。
。
∵CK:CF=2:3,设CK=2k,则CF=3k。
∴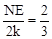 ,
,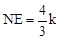 。
。
过N作NT∥EF交CF于T,
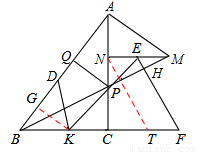
则四边形NTFE是平行四边形。
∴NE=TF=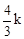 ,∴CT=CF-TF=3k-
,∴CT=CF-TF=3k- 。
。
∵EF⊥PM,∴∠BFH+∠HBF=90°=∠BPC+∠HBF。
∴∠BPC=∠BFH。
∵EF∥NT,∴∠NTC=∠BFH=∠BPC。
∴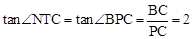 。
。
∴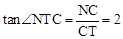 ,
,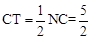 。
。
∴CT=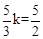 。∴
。∴ 。∴CK=2×
。∴CK=2×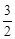 =3,BK=BC-CK=3。
=3,BK=BC-CK=3。
∵∠PKC+∠DKC=∠ABC+∠BDK,∠DKE=∠ABC,∴∠BDK=∠PKC。
∴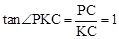 。∴tan∠BDK=1。
。∴tan∠BDK=1。
过K作KG⊥BD于G。
∵tan∠BDK=1,tan∠ABC=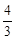 ,∴设GK=4n,则BG=3n,GD=4n。
,∴设GK=4n,则BG=3n,GD=4n。
∴BK=5n=3,∴n=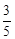 。∴BD=4n+3n=7n=
。∴BD=4n+3n=7n=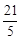 。
。
∵ ,AQ=4,∴BQ=AB-AQ=6。
,AQ=4,∴BQ=AB-AQ=6。
∴DQ=BQ-BD=6-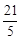 =
= 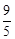 。
。
(1)确定一对全等三角形△AQP≌△MNA,得到AN=PQ;然后推出BP为角平分线,利用角平分线的性质得到PC=PQ;从而得到PC=AN。
(2)由已知条件,求出线段KC的长度,从而确定△PKC是等腰直角三角形;然后在△BDK中,解直角三角形即可求得BD、DQ的长度。


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:
 (1)化简:(a-
(1)化简:(a-| 1 |
| a |
| a2-2a+1 |
| a |
查看答案和解析>>
科目:初中数学 来源: 题型:
 20、如图,已知,在△ABC中,∠ABC和∠ACB的平分线交于点M,ME∥AB交BC于点E,MF∥AC交BC于点F.求证:△MEF的周长等于BC的长.
20、如图,已知,在△ABC中,∠ABC和∠ACB的平分线交于点M,ME∥AB交BC于点E,MF∥AC交BC于点F.求证:△MEF的周长等于BC的长.查看答案和解析>>
科目:初中数学 来源: 题型:
 已知:在△ABC中,∠B<∠C,AD平分∠BAC,AE⊥BC,垂足为点E.∠B=38°,∠C=70°.
已知:在△ABC中,∠B<∠C,AD平分∠BAC,AE⊥BC,垂足为点E.∠B=38°,∠C=70°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com