
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
分析 二次根式的定义:一般地,我们把形如$\sqrt{a}$(a≥0)的式子叫做二次根式.
解答 解:①$\sqrt{3}$符合二次根式的定义,故正确.
②$\sqrt{-5}$无意义,故错误.
③$\sqrt{a^2}$中的a2≥0,符合二次根式的定义,故正确.
④$\sqrt{x-1}$(x≥1)中的x-1≥0,符合二次根式的定义,故正确.
⑤$\root{3}{8}$是开3次方,故错误.
⑥$\sqrt{{x^2}+2x+1}$中的x2+2x+1=(x+1)2≥0,符合二次根式的定义,故正确.
故选:B.
点评 本题考查了二次根式的定义.理解被开方数是非负数,给出一个式子能准确的判断其是否为二次根式,并能根据二次根式的定义确定被开方数中的字母取值范围.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
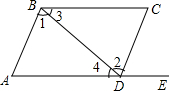 如图,给出下列条件:①∠1=∠2;②∠3=∠4;③∠A=∠CDE;④AD∥BC,且∠A=∠C.其中,能推出AB∥DC的条件为( )
如图,给出下列条件:①∠1=∠2;②∠3=∠4;③∠A=∠CDE;④AD∥BC,且∠A=∠C.其中,能推出AB∥DC的条件为( )| A. | ①④ | B. | ②③ | C. | ①③ | D. | ①③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图,P是正方形ABCD内一点,在正方形ABCD外有一点E,满足∠ABE=∠CBP,BE=BP.
已知:如图,P是正方形ABCD内一点,在正方形ABCD外有一点E,满足∠ABE=∠CBP,BE=BP.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,正方形ABCD的边长为1,点E在边AB上,连接ED,过点D作FD⊥DE与BC的延长线相交于点F,连接EF与边CD相交于点G、与对角线BD相交于点H.
如图,正方形ABCD的边长为1,点E在边AB上,连接ED,过点D作FD⊥DE与BC的延长线相交于点F,连接EF与边CD相交于点G、与对角线BD相交于点H.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com