
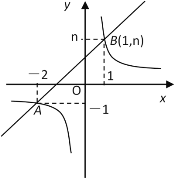
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于A(-2,-1)、B(1,n)两点。
的图象交于A(-2,-1)、B(1,n)两点。
(1)利用图中条件求反比例函数和一次函数的解析式;
(2)根据图象写出使一次函数的值大于反比例函数的值的![]() 的取值范围.
的取值范围.
科目:初中数学 来源: 题型:
【题目】某市为鼓励居民节约用水,采用分段计费的方法按月计算每户家庭的水费,月用水量不超过30立方米时,按2元/立方米计费;月用水量超过30立方米时,其中的30立方米仍按2元/立方米收费,超过部分按2.5元/立方米计费.设每户家庭月用水量为x立方米.
(1)当x不超过30时,应收多少水费(用x的代数式表示);当x超过30时,应收多少水费(用x的代数式表示);
(2)小明家四月份用水20立方米,五月份用水36立方米,请帮小明计算一下他家这两个月一共应交多少元水费?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在研究数学问题时遇到一个定义:将三个已经排好顺序的数:![]() ,
,![]() ,
,![]() ,称为数列
,称为数列![]() ,
,![]() ,
,![]() .计算
.计算![]() ,
,![]() ,
,![]() ,将这三个数的最小值称为数列
,将这三个数的最小值称为数列![]() ,
,![]() ,
,![]() 的最佳值.例如,对于数列2,
的最佳值.例如,对于数列2,![]() ,3,因为
,3,因为![]() ,
,![]() ,
,![]() ,所以数列2,
,所以数列2,![]() ,3的最佳值为
,3的最佳值为![]() .
.
小明进一步发现:当改变这三个数的顺序时,所得到的数列都可以按照上述方法计算其相应的最佳值.如数列![]() ,2,3的最佳值为
,2,3的最佳值为![]() ;数列3,
;数列3,![]() ,2的最佳值为1;
,2的最佳值为1;![]() .经过研究,小明发现,对于“2,
.经过研究,小明发现,对于“2,![]() ,3”这三个数,按照不同的排列顺序得到的不同数列中,最佳值的最小值为
,3”这三个数,按照不同的排列顺序得到的不同数列中,最佳值的最小值为![]() .根据以上材料,回答下列问题:
.根据以上材料,回答下列问题:
(1)求数列![]() ,
,![]() ,2的最佳值;
,2的最佳值;
(2)将“![]() ,
,![]() ,1”这三个数按照不同的顺序排列,可得到若干个数列,这些数列的最佳值的最小值为 ,取得最佳值最小值的数列为 (写出一个即可);
,1”这三个数按照不同的顺序排列,可得到若干个数列,这些数列的最佳值的最小值为 ,取得最佳值最小值的数列为 (写出一个即可);
(3)将3,![]() ,
,![]() 这三个数按照不同的顺序排列,可得到若干个数列.若使数列的最佳值为1,求
这三个数按照不同的顺序排列,可得到若干个数列.若使数列的最佳值为1,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
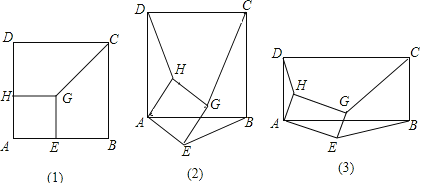
【题目】![]() 如图
如图![]() ,正方形AEGH的顶点E、H在正方形ABCD的边上,直接写出HD:GC:EB的结果______;
,正方形AEGH的顶点E、H在正方形ABCD的边上,直接写出HD:GC:EB的结果______;
![]() 将图
将图![]() 中的正方形AEGH绕点A旋转一定角度,如图
中的正方形AEGH绕点A旋转一定角度,如图![]() ,求HD:GC:EB;
,求HD:GC:EB;
![]() 把图
把图![]() 中的正方形都换成矩形,如图
中的正方形都换成矩形,如图![]() ,且已知DA:
,且已知DA:![]() :
:![]() ,求此时HD:GC:EB的值
,求此时HD:GC:EB的值![]() 简要写出过程
简要写出过程![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用棋子摆成如图所示的“T”字图案.

(1)摆成第一个“T”字需要多少枚棋子,第二个呢?按这样的规律摆下去,摆成第10个“T”字需要多少枚个棋子?
(2)第![]() 个需多少枚棋子?
个需多少枚棋子?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是△ABC的中线,E,F分别是AD和AD延长线上的点,且DE=DF,连结BF,CE.下列说法:①△ABD和△ACD面积相等;②∠BAD=∠CAD;③△BDF≌△CDE;④BF∥CE;其中正确的有( )
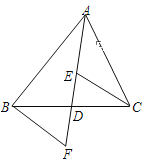
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
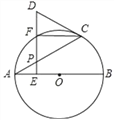
【题目】如图,AB是⊙O的直径,点P是弦AC上一动点(不与A,C重合),过点P作PE⊥AB,垂足为E,射线EP交弧AC于点F,交过点C的切线于点D.
(1)求证:DC=DP;
(2)若∠CAB=30°,当F是弧AC的中点时,判断以A,O,C,F为顶点的四边形是什么特殊四边形?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ABC=90°,AB=BC=4,将△ABC△绕点A顺时针旋转60°,得到△ADE,连结BE,则BE的长为_____.
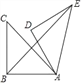
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料,根据材料回答:
例如1:![]()
![]()
![]()
![]()
![]() .
.
例如2:
8![]() ×0.125
×0.125![]() =8×8×8×8×8×8×0.125×0.125×0.125×0.125×0.125×0.125
=8×8×8×8×8×8×0.125×0.125×0.125×0.125×0.125×0.125
=(8×0.125)×(8×0.125)×(8×0.125)×(8×0.125)×(8×0.125)×(8×0.125)
=(8×0.125)6 =1.
(1)仿照上面材料的计算方法计算:![]() ;
;
(2)由上面的计算可总结出一个规律:(用字母表示) ![]() ;
;
(3)用(2)的规律计算:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com