
【题目】已知△ABC中,∠ACB=90°,将AB边绕点B顺时针旋转90°得线段BD.过点D作DM⊥BC交BC延长线于M,
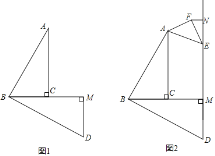
(1)如图1,请判断线段AC、CM、MD的数量关系并说明理由;
(2)E为DM延长线上一点,当点E为如图2所示的位置时,以AE为斜边向右侧作等腰Rt△AFE,再过点F作FN⊥DM于N,探究BM、FN、MN三条线段的数量关系,并说明理由;
(3)在问题(2)的条件下,当点E运动到某一位置时点B、A、F三点恰好在同一直线上,取DE中点P,连接AP,且AB=3,AF=1,请直接写出AP的值.
【答案】(1)AC=MD+MC,理由见解析;(2)MN=FN+BM,理由见解析;(3)![]()
【解析】
(1)由旋转的性质可得AB=BD,∠ABD=90°,由“AAS”可证△ABC≌△BDM,可得AC=BM,BC=MD,可证AC=MD+MC;
(2)如图2,延长NF,CA交于点H,可证四边形HCMN是矩形,可得MN=HC,∠H=90°,由“AAS”可证△AFH≌△FEN,可得AH=FN,可得结论;
(3)如图3,过点A作AG⊥MN,由相似三角形的性质可得BC=3HF,AC=3AH,由勾股定理可求HF、AH、PE,再利用勾股定理即可求得答案.
(1)AC=MD+MC,
理由如下:
∵将AB边绕点B顺时针旋转90°得线段BD,
∴AB=BD,∠ABD=90°,
∴∠ACB=∠ABD=90°,
∴∠A+∠ABC=90°,∠ABC+∠DBM=90°,
∴∠A=∠DBM,
在△ABC和△BDM中,
 ,
,
∴△ABC≌△BDM(AAS)
∴AC=BM,BC=MD,
∵BM=BC+CM,
∴AC=MD+MC;
(2)MN=FN+BM,
理由如下:
如图2,延长NF,CA交于点H,
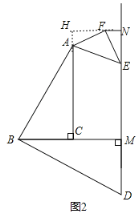
∵∠ACM=∠BMN=90°,FN⊥MN,
∴四边形HCMN是矩形,
∴MN=HC,∠H=90°,HN=CM,
∵△AEF是等腰直角三角形,
∴AF=EF,∠AFE=90°=∠H,
∴∠HFA+∠HAF=90°,∠HFA+∠NFE=90°,
∴∠NFE=∠HAF,
在△AFH和△FEN中,
 ,
,
∴△AFH≌△FEN(AAS)
∴AH=FN,
∵MN=HC=AC+AH,
∴MN=FN+BM;
(3)如图3,延长NF,CA交于点H,过点A作AG⊥MN,

∵∠ACM=∠BMN=90°,FN⊥MN,AG⊥MN,
∴四边形HCMN、ACMG、AGNH是矩形,
∴AG=HN,AH=NG,MN=CH,
∵FN⊥MN,DM⊥BC,
∴NH∥BM,
∴△ABC∽△AFH,
∴![]() ,
,
∴BC=3HF,AC=3AH,
由(2)得:CM=HN,AH=FN,FH=EN,AC=BM,
∴AC﹣BC= BM﹣BC=CM=HN=FH+FN,
∴3AH﹣3HF=HF+AH,
∴AH=2HF,
∵AH2+HF2=AF2=1,
∴HF=![]() ,AH=
,AH=![]() ,
,
∴HN=![]() ,BC=
,BC=![]() =MD,AC=
=MD,AC=![]() ,MN=CH= AC+ AH=
,MN=CH= AC+ AH=![]() ,
,
∴DE=MD+MN﹣NE=![]() ,
,
∵点P是DE中点,
∴PE=![]() ,
,
∴AG=HN=![]() ,AH=NG=
,AH=NG=![]() ,
,
∴EG= NG- EN= NG- HF=![]() ,
,
∴GP=EP﹣EG=![]() ,
,
∴ .
.


科目:初中数学 来源: 题型:
【题目】从﹣1,﹣2,﹣3,﹣4,﹣5,﹣6中任取一个数作为k的值,则能使分式方程![]() 有非负实数解且使二次函数y=x2+2x﹣k﹣1的图象与x轴无交点的概率为( )
有非负实数解且使二次函数y=x2+2x﹣k﹣1的图象与x轴无交点的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.0
D.0
查看答案和解析>>
科目:初中数学 来源: 题型:
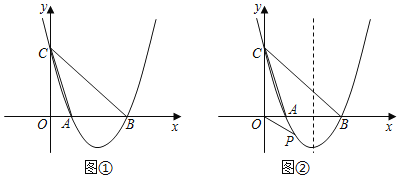
【题目】如图①,已知抛物线y=ax2﹣4amx+3am2(a、m为参数,且a>0,m>0)与x轴交于A、B两点(A在B的左边),与y轴交于点C.
(1)求点B的坐标(结果可以含参数m);
(2)连接CA、CB,若C(0,3m),求tan∠ACB的值;
(3)如图②,在(2)的条件下,抛物线的对称轴为直线l:x=2,点P是抛物线上的一个动点,F是抛物线的对称轴l上的一点,在抛物线上是否存在点P,使△POF成为以点P为直角顶点的的等腰直角三角形.若存在,求出所有符合条件的点P的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
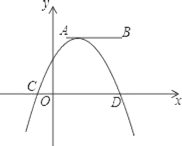
【题目】如图,点A,B的坐标分别为(1,4)和(4,4),抛物线y=a(x+m)2+n的顶点在线段AB上,与x轴交于C,D两点(C在D的左侧),点C的横坐标最小值为﹣3,则点D的横坐标的最大值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】广州火车南站广场计划在广场内种植A,B两种花木共 6600棵,若A花木数量是B花木数量的2倍少600棵.
(1)A,B两种花木的数量分别是多少棵?
(2)如果园林处安排26人同时种植这两种花木,每人每天能种植A花木60棵或B花木40棵,应分别安排多少人种植A花木和B花木,才能确保同时完成各自的任务?
查看答案和解析>>
科目:初中数学 来源: 题型:
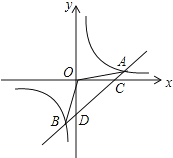
【题目】如图,一次函数y=x+b和反比例函数y=![]() (k≠0)交于点A(4,1).
(k≠0)交于点A(4,1).
(1)求反比例函数和一次函数的解析式;
(2)求△AOB的面积;
(3)根据图象直接写出一次函数的值大于反比例函数的值的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年春节,小娜家购买了4个灯笼,灯笼上分别写有“欢”、“度”、“春”、“节”(外观完全一样).
(1)小娜抽到“2019年”是 事件,“欢”字被抽中的是 事件;(填“不可能”或“必然”或“随机”).小娜从四个灯笼中任取一个,取到“春”的概率是 .
(2)小娜从四个灯笼中先后取出两个灯笼,请用列表法或画树状图法求小娜恰好取到“春”、“节”两个灯笼的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
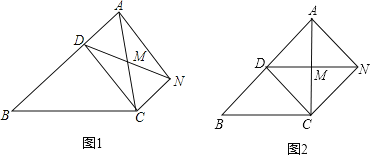
【题目】已知,如图1,D是△ABC的边上一点,CN∥AB,DN交AC于点M,MA=MC.
(1)求证:四边形ADCN是平行四边形.
(2)如图2,若∠AMD=2∠MCD,∠ACB=90°,AC=BC.请写出图中所有与线段AN相等的线段(线段AN除外)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com