
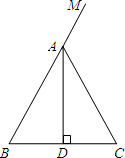
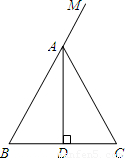
 已知:有一纸片如图,其中△ABC中,AD⊥BC,垂足为点D,BD=CD,点M在BA的延长线上.实施操作:将纸片沿一直线AN折叠,使AM和AC重合,并且过点C作CE⊥AN,垂足为点E.
已知:有一纸片如图,其中△ABC中,AD⊥BC,垂足为点D,BD=CD,点M在BA的延长线上.实施操作:将纸片沿一直线AN折叠,使AM和AC重合,并且过点C作CE⊥AN,垂足为点E. (1)解:如图所示:
(1)解:如图所示: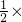 180°=90°.
180°=90°. BC,由已知可得,DC=
BC,由已知可得,DC= BC,由(2)的结论可知四边形ADCE为矩形,所以证得,四边形ADCE为正方形.
BC,由(2)的结论可知四边形ADCE为矩形,所以证得,四边形ADCE为正方形.

 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•路南区一模)已知:有一纸片如图,其中△ABC中,AD⊥BC,垂足为点D,BD=CD,点M在BA的延长线上.实施操作:将纸片沿一直线AN折叠,使AM和AC重合,并且过点C作CE⊥AN,垂足为点E.
(2012•路南区一模)已知:有一纸片如图,其中△ABC中,AD⊥BC,垂足为点D,BD=CD,点M在BA的延长线上.实施操作:将纸片沿一直线AN折叠,使AM和AC重合,并且过点C作CE⊥AN,垂足为点E.查看答案和解析>>
科目:初中数学 来源:2012年河北省唐山市路南区中考数学一模试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com