
【题目】如图,分别以直角△ABC的斜边AB,直角边AC为边向△ABC外作等边△ABD和等边△ACE,F为AB的中点,DE与AB交于点G,EF与AC交于点H,∠ACB=90°,∠BAC=30°.给出如下结论:①EF⊥AC;②四边形ADFE为菱形;③AD=4AG;其中正确结论的为(请将所有正确的序号都填上).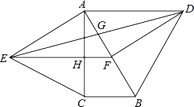
【答案】①③
【解析】解:∵△ACE是等边三角形,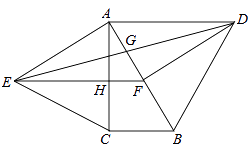
∴∠EAC=60°,AE=AC,
∵∠BAC=30°,
∴∠FAE=∠ACB=90°,AB=2BC,
∵F为AB的中点,
∴AB=2AF,
∴BC=AF,
∴△ABC≌△EFA,
∴FE=AB,
∴∠AEF=∠BAC=30°,
∴EF⊥AC,故①正确,
∵EF⊥AC,∠ACB=90°,
∴HF∥BC,
∵F是AB的中点,
∴HF= ![]() BC,
BC,
∵BC= ![]() AB,AB=BD,
AB,AB=BD,
∴HF= ![]() BD,故④说法正确;
BD,故④说法正确;
∵AD=BD,BF=AF,
∴∠DFB=90°,∠BDF=30°,
∵∠FAE=∠BAC+∠CAE=90°,
∴∠DFB=∠EAF,
∵EF⊥AC,
∴∠AEF=30°,
∴∠BDF=∠AEF,
∴△DBF≌△EFA(AAS),
∴AE=DF,
∵FE=AB,
∴四边形ADFE为平行四边形,
∵AE≠EF,
∴四边形ADFE不是菱形;
故②说法不正确;
∴AG= ![]() AF,
AF,
∴AG= ![]() AB,
AB,
∵AD=AB,
则AD=4AG,故③说法正确,
故答案为①③。
根据已知先判断△ABC≌△EFA,则∠AEF=∠BAC,得出EF⊥AC,由等边三角形的性质得出∠BDF=30°,从而证得△DBF≌△EFA,则AE=DF,再由FE=AB,得出四边形ADFE为平行四边形而不是菱形,根据平行四边形的性质得出AD=4AG,从而得到答案.


科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是边长为a的正方形,点G、E分别是边AB、BC的中点,∠AEF=90°,且EF交正方形外角的平方线CF于点F.
(1)证明:△AGE≌△ECF;
(2)求△AEF的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.必然事件发生的概率为0
B.一组数据1,6,3,9,8的极差为7
C.“面积相等的两个三角形全等”这一事件是必然事件
D.“任意一个三角形的外角和等于180°”这一事件是不可能事件
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王老师将1个黑球和若干个白球放入一个不透明的口袋并搅匀,让若干学生进行摸球实验,每次摸出一个球(有放回),下表是活动进行中的一组部分统计数据.
摸球的次数 | 100 | 150 | 200 | 500 | 800 | 1000 |
摸到黑球的次数 | 23 | 31 | 60 | 127 | 203 | 251 |
摸到黑球的频率 | 0.23 | 0.21 | 0.30 | 0.254 | 0.253 |
|
(1)根据上表数据计算 ![]() = . 估计从袋中摸出一个球是黑球的概率是 . (精确到0. 01)
= . 估计从袋中摸出一个球是黑球的概率是 . (精确到0. 01)
(2)估算袋中白球的个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在□ABCD,∠ABC的平分线交AD于点E,延长BE交CD的延长线于F.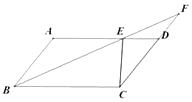
(1)若∠F=20°,求∠A的度数;
(2)若AB=5,BC=8,CE⊥AD,求□ABCD的面积;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com