
【题目】如图,抛物线y=﹣x2+bx+c与x轴交于A(1,0),B(﹣3,0)
(1)求这条抛物线的解析式;
(2)设(1)中的抛物线交y轴于C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出点Q的坐标;若不存在说明理由;
【答案】
(1)解:抛物线的解析式为y=﹣(x﹣1)(x+3),即y=﹣x2﹣2x+3;
(2)解:存在.
当x=0时,y=﹣x2﹣2x+3=3,则C(0,3),
抛物线的对称轴为直线x=﹣1,
连接BC交直线x=﹣1于Q,如图,
∵点A与点B关于直线x=﹣1对称,
∴QA=QB,
∴QA+QC=QB+QC=BC,
∴此时QA+QC的值最小,
∴此时△QAC的周长最小,
设直线BC的解析式为y=kx+b,
把B(﹣3,0),C(0,3)代入得 ![]() ,解得
,解得 ![]() ,
,
∴直线BC的解析式为y=x+3,
当x=﹣1时,y=x+3=2,
∴满足条件的Q点的坐标为(﹣1,2);

;(3)(1)中抛物线在第二象限的图象是否存在一点P,使得△PBC的面积最大?若存在,求出点P的坐标及△PBC面积的最大值;若不存在,请说明理由.
解:存在.
过PD∥y轴交BC于P,如图,
设P(x,﹣x2﹣2x+3)(﹣3<x<0),则D(x,x+3),
∴PD=﹣x2﹣2x+3﹣(x+3)=﹣x2﹣3x,
∴S△PBC=S△PBD+S△PCD= ![]() 3PD=﹣
3PD=﹣ ![]() x2﹣
x2﹣ ![]() x=﹣
x=﹣ ![]() (x+
(x+ ![]() )2+
)2+ ![]() ,
,
当x=﹣ ![]() 时,S△PBC值最大,最大值为
时,S△PBC值最大,最大值为 ![]() ,
,
此时P点坐标为(﹣ ![]() ,
, ![]() ).
).
【解析】(1)利用交点式可直接得到抛物线的解析式;(2)先确定C(0,3),抛物线的对称轴为直线x=﹣1,连接BC交直线x=﹣1于Q,如图,利用两点之间线段最短解决最短路径问题得到此时QA+QC的值最小,从而确定此时△QAC的周长最小,再利用待定系数法求出直线BC的解析式为y=x+3,然后计算自变量为﹣1时的一次函数值即可得到满足条件的Q点的坐标;(3)过PD∥y轴交BC于P,如图,设P(x,﹣x2﹣2x+3)(﹣3<x<0),则D(x,x+3),则PD可表示为﹣x2﹣3x,利用三角形面积公式得到S△PBC=﹣ ![]() x2﹣
x2﹣ ![]() x,然后利用二次函数的性质求解.
x,然后利用二次函数的性质求解.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,将1, ![]() ,
, ![]() ,
, ![]() 按下列方式排列.若规定(m,n)表示第m排从左向右第n个数,则(5,4)与(15,2)表示的两数之积是 _________.
按下列方式排列.若规定(m,n)表示第m排从左向右第n个数,则(5,4)与(15,2)表示的两数之积是 _________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一个能自由转动的正六边形转盘,这个转盘被三条分割线分成形状相同,面积相等的三部分,且分别标有“1”、“2”、“3”三个数字,指针的位置固定不动,让转盘自由转动两次,当每次转盘停止后,记录指针指向的数(当指针指向分割线时,视其指向分割线左边的区域),则两次指针指向的数都是奇数的概率为 . 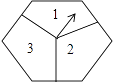
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学现有学生2870人,学校为了进一步丰富学生课余生活,拟调整兴趣活动小组,为此进行了一次抽样调查,根据采集到的数据绘制的统计图(不完整)如下:

请你根据图中提供的信息,完成下列问题:
(1)图1中,“电脑”部分所对应的圆心角为 _________ 度;
(2)共抽查了 _________ 名学生;
(3)在图2中,将“体育”部分的图形补充完整;
(4)爱好“书画”的人数占被调查人数的百分比 _________ ;
(5)估计现有学生中,有 _________ 人爱好“书画”.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为缓解“停车难”的问题,某单位拟造地下停车库,建筑设计师提供了该地下停车库的设计示意图如图所示,已知该坡道的水平距离AB的长为9m,坡面AD与AB的夹角∠BAD=18°,石柱BC=0.5m,按规定,地下停车库坡道上方BC处要张贴限高标志,以便告知停车人车辆能否安全驶入.请你帮设计师计算一下CE的高度,以便张贴限高标志,结果精确到0.1m.
(参考数值:sin72°≈0.95,cos72°≈0.31,tan72°≈3.08,sin18°≈0.31,cos18°≈0.95,tan18°≈0.32)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在△ABC中,∠ABC=3∠C,∠BAC的平分线AD交BC于D,BE⊥AD于E.
(1)如图l,求证:AC﹣AB=2BE.
(2)如图2,将∠DCA沿直线AC翻折,交BA的延长线于点M,连接MD交AC于点N;MA=BA,BE=1,AB=![]() ,求AN的长.
,求AN的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了推动阳光体育运动的广泛开展,引导学生走向操场,积极参加体育锻炼,学校准备购买一批运动鞋供学生借用,现从各年级随机抽取了部分学生的鞋号,绘制了统计图①和图②,请根据相关信息,解答下列问题:
(1)本次接受随机抽样调查的学生人数为______,图①中![]() 的值为_____;
的值为_____;
(2)本次调查获取的样本数据的众数为______,中位数为________;
(3)根据样本数据,若学校计划购买200双运动鞋,建议购买35号运动鞋多少双?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的顶点坐标为(4,﹣ ![]() ),且与y轴交于点C(0,2),与x轴交于A,B两点(点A在点B的左边).
),且与y轴交于点C(0,2),与x轴交于A,B两点(点A在点B的左边).
(1)求抛物线的解析式及A、B两点的坐标;
(2)在(1)中抛物线的对称轴l上是否存在一点P,使AP+CP的值最小?若存在,求AP+CP的最小值,若不存在,请说明理由;
(3)以AB为直径的⊙M相切于点E,CE交x轴于点D,求直线CE的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,真命题是( )
A. 如果三角形三个角的度数比是3:4:5,那么这个三角形是直角三角形
B. 如果直角三角形两直角边的长分别为a和b,那么斜边的长为a2+b2
C. 若三角形三边长的比为1:2:3,则这个三角形是直角三角形
D. 如果直角三角形两直角边分别为a和b,斜边为c,那么斜边上的高h的长为![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com