
画出函数 的图象,利用图象:
的图象,利用图象:
(1)求方程 的解;
的解;
(2)求不等式 的解;
的解;
(3)若 ,求
,求 的取值范围。
的取值范围。
(1)x=-2;(2)x<-2;(3)-3≤x≤1.
解析试题分析:首先求出直线与坐标轴的交点坐标,经过两点画直线.然后观察图象即可求得答案.
(1)方程2x+4=0的解是指直线与x轴的交点坐标;
(2)不等式2x+4<0的解是指y<0的部分;
(3)当-2≤y≤6,找到对应的点,即可求得x的取值范围.
试题解析:当x=0时,y=4,当y=0时,x=-2,
∴A(0,4),B(-2,0),
作直线AB:
(1)由图象得:方程2x+4=0的解为:x=-2;
(2)由图象得:不等式2x+4<0的解为:x<-2;
(3)由图象得:-2≤y≤6,x的取值范围为:-3≤x≤1.
考点:1.一次函数的图象;2.一次函数与一元一次方程;3.一次函数与一元一次不等式.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
如图,已知二次函数y=x -4x+3的图象交x轴于A,B两点(点A在点B的左侧), 交y轴于点C.
-4x+3的图象交x轴于A,B两点(点A在点B的左侧), 交y轴于点C.
(1)求直线BC的解析式;
(2)点D是在直线BC下方的抛物线上的一个动点,当△BCD的面积最大时,求D点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
小文家与学校相距1000米,某天小文上学时忘了带一本书,走了一段时间才想起,于是返回家拿书,然后加快速度赶到学校,下图是小文与家的距离y(米)关于时间x(分钟)的函数图象。请你根据图象中给出的信息,解答下列问题: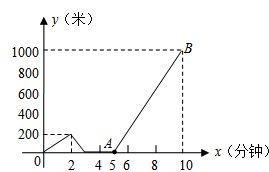
(1)小文走了多远才返回家拿书?
(2)求线段AB所在直线的函数解析式;
(3)当x=8分钟时,求小文与家的距离。
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在平面直角坐标系中,矩形OABC的顶点A在y轴正半轴上,点B的横、纵坐标分别是一元二次方程x2+5x﹣24=0的两个实数根,点D是AB的中点.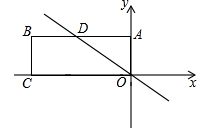
(1)求点B坐标;
(2)求直线OD的函数表达式;
(3)点P是直线OD上的一个动点,当以P、A、D三点为顶点的三角形是等腰三角形时,请直接写出P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,已知反比例函数 与一次函数
与一次函数 的图象在第一象限相交于点A(1,
的图象在第一象限相交于点A(1, ),
),
(1)试确定这两个函数的表达式;
(2)求出这两个函数图像的另一个交点B的坐标,并根据图象写出使一次函数的值小于反比例函数值的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,函数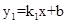 的图象与函数
的图象与函数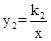 (
(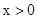 )的图象交于点A(2,1)、B,与y轴交于点C(0,3).
)的图象交于点A(2,1)、B,与y轴交于点C(0,3).
(1)求函数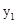 的表达式和点B的坐标;
的表达式和点B的坐标;
(2)观察图象,比较当x>0时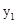 与
与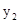 的大小.
的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
某软件公司开发出一种图书管理软件,前期投入的各种费用总共50000元,之后每售出一套软件,软件公司还需支付安装调试费用200元,设销售套数x(套)。
(1)试写出总费用y(元)与销售套数x(套)之间的函数关系式.
(2)该公司计划以400元每套的价格进行销售,并且公司仍要负责安装调试,试问:软件公司售出多少套软件时,收入超出总费用?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
我国是一个严重缺水的国家.为了加强公民的节水意识,某市制定了如下用水收费标准:每户每月的用水不超过6吨时,水价为每吨2元,超过6吨时,超过的部分按每吨3元收费.该市某户居民5月份用水 吨,应交水费
吨,应交水费 元.
元.
(1)若0< ≤6,请写出
≤6,请写出 与
与 的函数关系式.(3分)
的函数关系式.(3分)
(2)若 >6,请写出
>6,请写出 与
与 的函数关系式.(3分)
的函数关系式.(3分)
(3)在同一坐标系下,画出以上两个函数的图象.(4分)
(4)如果该户居民这个月交水费27元,那么这个月该户用了多少吨水?(4分)
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
(2013年四川攀枝花12分)如图,在平面直角坐标系中,四边形ABCD是梯形,AB∥CD,点B(10,0),C(7,4).直线l经过A,D两点,且sin∠DAB= .动点P在线段AB上从点A出发以每秒2个单位的速度向点B运动,同时动点Q从点B出发以每秒5个单位的速度沿B→C→D的方向向点D运动,过点P作PM垂直于x轴,与折线A→D→C相交于点M,当P,Q两点中有一点到达终点时,另一点也随之停止运动.设点P,Q运动的时间为t秒(t>0),△MPQ的面积为S.
.动点P在线段AB上从点A出发以每秒2个单位的速度向点B运动,同时动点Q从点B出发以每秒5个单位的速度沿B→C→D的方向向点D运动,过点P作PM垂直于x轴,与折线A→D→C相交于点M,当P,Q两点中有一点到达终点时,另一点也随之停止运动.设点P,Q运动的时间为t秒(t>0),△MPQ的面积为S.
(1)点A的坐标为 ,直线l的解析式为 ;
(2)试求点Q与点M相遇前S与t的函数关系式,并写出相应的t的取值范围;
(3)试求(2)中当t为何值时,S的值最大,并求出S的最大值;
(4)随着P,Q两点的运动,当点M在线段DC上运动时,设PM的延长线与直线l相交于点N,试探究:当t为何值时,△QMN为等腰三角形?请直接写出t的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com