
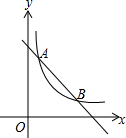
 如图,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$(m≠0)的图象交于A(6,1),B(a,6)两点.
如图,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$(m≠0)的图象交于A(6,1),B(a,6)两点.分析 (1)首先由A(6,1)在反比例函数y=$\frac{m}{x}$(m≠0)的图象上,求得反比例函数的解析式,即可求得点B的坐标,再将A,B代入一次函数解析式,即可求得答案;
(2)观察图形,一次函数的值大于反比例函数的值,即在第一象限内,一次函数在反比例函数上面的部分.
解答 解:(1)∵A(6,1)在反比例函数y=$\frac{m}{x}$(m≠0)的图象上,
∴m=xy=6×1=6,
∴反比例函数的解析式为:y=$\frac{6}{x}$;
∵B(a,6)在反比例函数y=$\frac{6}{x}$的图象上,
∴6=$\frac{6}{a}$,
解得:a=1,
∴B的坐标为(1,6),
∴$\left\{\begin{array}{l}{6k+b=1}\\{k+b=6}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-1}\\{b=7}\end{array}\right.$,
∴一次函数的解析式为:y=-x+7;
(2)观察图象得:在第一象限内,当1<x<6时,一次函数的值大于反比例函数的值.
点评 此题考查了反比例函数与一次函数的交点问题.注意掌握待定系数法的应用是关键.


科目:初中数学 来源: 题型:解答题
 某学校教学楼从一楼到二楼由两段坡度相等的楼梯CA、AB联通(如图),经测量的这两层楼间的垂直高度BC为5米,∠BAC=70°,试求一楼到二楼的楼梯总长度(精确到0.1米).
某学校教学楼从一楼到二楼由两段坡度相等的楼梯CA、AB联通(如图),经测量的这两层楼间的垂直高度BC为5米,∠BAC=70°,试求一楼到二楼的楼梯总长度(精确到0.1米).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
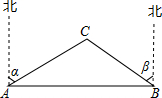 如图,已知A、B两市相距150千米,分别从A、B处测得某风景区中心C处的方向角如图所示,风景区区域是以C为圆心,52千米为半径的圆,tanα≈1.63,tanβ≈1.37.有关部门要设计修建连接AB两市的高速公路,问连接AB的高速公路是否穿过风景区,请说明理由.
如图,已知A、B两市相距150千米,分别从A、B处测得某风景区中心C处的方向角如图所示,风景区区域是以C为圆心,52千米为半径的圆,tanα≈1.63,tanβ≈1.37.有关部门要设计修建连接AB两市的高速公路,问连接AB的高速公路是否穿过风景区,请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
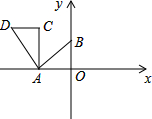 如图,直线y=$\frac{3}{4}$x+3与x轴、y轴分别交于A、B两点,把△AOB绕点A逆时针旋转90°后得到△ACD,则点D的坐标是( )
如图,直线y=$\frac{3}{4}$x+3与x轴、y轴分别交于A、B两点,把△AOB绕点A逆时针旋转90°后得到△ACD,则点D的坐标是( )| A. | (4,3) | B. | (-3,4) | C. | (-7,4) | D. | (-7,3) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
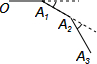 如图,小敏从点0出发,前进10 m到达点A1后,向右转30°前进10m到达点A2,再向
如图,小敏从点0出发,前进10 m到达点A1后,向右转30°前进10m到达点A2,再向查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | P(C)<P(A)<P(B) | B. | P(B)<P(C)<P(A) | C. | P(C)<P(B)<P(A) | D. | P(B)<P(A)<P(C) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com