
【题目】在下列命题中:(1)抛物线y=2(x﹣3)2﹣6顶点坐标是(3,﹣6);(2)一元二次方程x2﹣2x+![]() =0的两根之和等于2;(3)已知抛物线y=ax2+bx+c(a<0)的对称轴为x=﹣2,与x轴的一个交点为(2,0).若关于x的一元二次方程ax2+bx+c=p(p>0)有整数根,则p的值有4个;(4)二次函数y=﹣x2﹣2x+c在﹣3≤x≤2的范围内有最小值﹣5,则c的值是﹣2.其中正确结论的个数是( )
=0的两根之和等于2;(3)已知抛物线y=ax2+bx+c(a<0)的对称轴为x=﹣2,与x轴的一个交点为(2,0).若关于x的一元二次方程ax2+bx+c=p(p>0)有整数根,则p的值有4个;(4)二次函数y=﹣x2﹣2x+c在﹣3≤x≤2的范围内有最小值﹣5,则c的值是﹣2.其中正确结论的个数是( )
A.1个B.2个C.3个D.4个
【答案】C
【解析】
(1)根据抛物线的顶点坐标即可判断;
(2)根据一元二次方程根与系数的关系即可判断;
(3)根据抛物线开口向下,与x轴的交点坐标为(2,0)(﹣6,0),在x轴上方当x能取几个整数解时对应的y的值就有几个即可判断;
(4)先将c=﹣2代入解析式,再计算x=﹣3和x=2时比较y的最小值即可判断.
(1)抛物线y=2(x﹣3)2﹣6顶点坐标是(3,﹣6),所以(1)正确;
(2)一元二次方程x2﹣2x+![]() =0的两根之和等于2,所以(2)正确;
=0的两根之和等于2,所以(2)正确;
(3)∵抛物线y=ax2+bx+c(a<0)
∴开口向下,
对称轴为x=﹣2,与x轴的一个交点为(2,0).
所以抛物线与x轴的另一个交点为(﹣6,0),
关于x的一元二次方程ax2+bx+c=p(p>0)有整数根,
根据图象可知:x的值为1,0,﹣1,﹣2,
所以p的值有4个;所以(3)正确;
(4)当c=﹣2时,y=﹣x2﹣2x﹣2,
当x=﹣3时,y=﹣5,
当x=2时,y=﹣8,
∵a=﹣1<0,
抛物线开口向下,
∴在﹣3≤x≤2的范围内有最小值﹣8,所以(4)错误.
综上:(1)(2)(3)正确,共3个;
故选:C.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC是等腰三角形,且AC=BC,∠ACB=120°,在AB上取一点O,使OB=OC,以O为圆心,OB为半径作圆,过C作CD∥AB交⊙O于点D,连接BD.
(1)猜想AC与⊙O的位置关系,并证明你的猜想;
(2)已知AC=6,求扇形OBC围成的圆锥的底面圆半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级学生在一起射击训练中,随机抽取10名学生的成绩如下表,回答问题:
环数 | 6 | 7 | 8 | 9 |
人数 | 1 | 5 | 2 |
|
(1)填空:![]() _______;
_______;
(2)10名学生的射击成绩的众数是_______环,中位数是_______环;
(3)若9环(含9环)以上评为优秀射手,试估计全年级500名学生中有_______名是优秀射手.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,BD平分∠ABC.求作⊙O,使得点O在边AB上,且⊙O经过B、D两点;并证明AC与⊙O相切.(尺规作图,保留作图痕迹,不写作法)

查看答案和解析>>
科目:初中数学 来源: 题型:
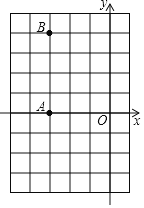
【题目】坐标为整数的点叫格点,如图,已知A(-3,0)、B(-3,4)和原点都是格点,在如图6×9的网格中使用无刻度的直尺按要求作图.
(1)找格点C,连BC,使BC与OA的交点就是OA的中点,画出图形直接写出C点坐标.
(2)按以下方法可以作出∠AOB的平分线.
第一步:找格点D,使OD=OB;
第二步:找格点E,使DE⊥OB交AB于F;
第三步:连OF,则OF是∠AOB的平分线;
请你按步骤完成作图,并写出D、E三点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,点
中,点![]() 的坐标为(
的坐标为(![]() ,
,![]() ),点
),点![]() 的坐标为(
的坐标为(![]() ,
,![]() ),点C的坐标为(
),点C的坐标为(![]() ,
,![]() ).
).
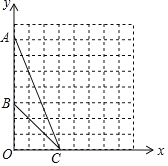
(1)在图中作出![]() 的外接圆(利用格图确定圆心);
的外接圆(利用格图确定圆心);
(2)圆心坐标为 _____;外接圆半径![]() 为 _____;
为 _____;
(3)若在![]() 轴的正半轴上有一点
轴的正半轴上有一点![]() ,且
,且![]() ,则点
,则点![]() 的坐标为 _____.
的坐标为 _____.
查看答案和解析>>
科目:初中数学 来源: 题型:
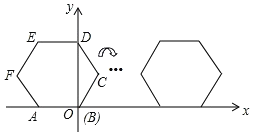
【题目】如图,将正六边形ABCDEF放置在直角坐标系内,A(﹣2,0),点B在原点,把正六边形ABCDEF沿x轴正半轴作无滑动的连续翻转,每次翻转60°,经过2020次翻转之后,点C的坐标是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工程对承接了60万平方米的绿化工程,由于情况有变,……,设原计划每天绿化的面积为![]() 万平方米,列方程为
万平方米,列方程为![]() ,根据方程可知省略的部分是( )
,根据方程可知省略的部分是( )
A.实际工作时每天的工作效率比原计划提高了20%,结果提前30天完成了这一任务
B.实际工作时每天的工作效率比原计划提高了20%,结果延误30天完成了这一任务
C.实际工作时每天的工作效率比原计划降低了20%,结果延误30天完成了这一任务
D.实际工作时每天的工作效率比原计划降低了20%,结果提前30天完成了这一任务
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com