
【题目】如图,A、B是反比例函数y=![]() 上两点,AC⊥y轴于C,BD⊥x轴于D,AC=BD=
上两点,AC⊥y轴于C,BD⊥x轴于D,AC=BD=![]() OC,S四边形ABDC=14,则k= .
OC,S四边形ABDC=14,则k= .

【答案】16.
【解析】
试题分析:利用已知条件判断点A与点B的纵横坐标正好相反,从而设出点A的坐标,进而求得点B的坐标,利用SACDB=S△CED-S△AEB,求得点A的坐标后,用待定系数法确定出k的值.
试题解析:如图,分别延长CA,DB交于点E,根据AC⊥y轴于C,BD⊥x轴于D,AC=BD=![]() OC,
OC,
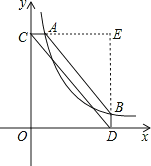
知△CED为直角三角形,且点A与点B的纵横坐标正好相反,
设点A的坐标为(xA,yA),则点B的坐标为(yA,xA),点E的坐标为(yA,yA),
四边形ACDB的面积为△CED的面积减去△AEB的面积.
CE=ED=yA,AE=BE=y-![]() yA,
yA,
∴SACDB=S△CED-S△AEB=![]() [yAyA-(yA-
[yAyA-(yA-![]() yA)(yA-
yA)(yA-![]() yA)]=
yA)]=![]() yA2=14,
yA2=14,
∵yA>0,∴yA=8,
点A的坐标为(2,8),
∴k=2×8=16.


科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2-4x+3与x轴相交于点A,B(点A在点B左侧),顶点为M.平移该抛物线,使点M平移后的对应点M'落在x轴上,点B平移后的对应点B'落在y轴上.则平移后的抛物线解析式为 ( )
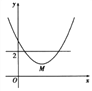
A. y=x2+2x+1 B. y=x2+2x-1 C. y=x2-2x+1 D. y=x2-2x-1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中每个小正方形的边长都是1个单位长度,Rt△ABC的三个顶点A(-2,2),B(0,5),C(0,2).
(1)将△ABC以点C为旋转中心旋转180°,得到△A1B1C,请画出△A1B1C的图形.
(2)平移△ABC,使点A的对应点A2坐标为(-2,-6),请画出平移后对应的△A2B2C2的图形.
(3)若将△A1B1C绕某一点旋转可得到△A2B2C2,请直接写出旋转中心的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市举办中学生“梦想杯”足球联赛,联赛记分办法是:胜1场得3分,平1场得1分,负1场得0分.复兴中学足球队参加了18场比赛,积24分.
(1)在这次足球联赛中,如果复兴中学足球队踢平场数与所负场数相同,那么它胜了几场?
(2)在这次足球联赛中,如果复兴中学足球队踢平场数多于所负场数,那么它的胜、平、负情况共有多少种?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠A=52°,∠ABC与∠ACB的角平分线交于D1, ∠ABD1与∠ACD1的角平分线交于点D2,依次类推,∠ABD4与∠ACD4 的角平分线交于点D5,则∠BD5C的度数是( )

A. 56°;B. 60°;C. 68°;D. 94°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() ,
,![]() 是一次函数
是一次函数![]() 的图象和反比例函数
的图象和反比例函数![]() 的图象的两个交点.
的图象的两个交点.
(1)求一次函数、反比例函数的关系式;
(2)求△AOB的面积
(3) 当自变量x满足什么条件时,![]() >
>![]() .(直接写出答案)
.(直接写出答案)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,圆桌正上方的灯泡(看作一个点)发出的光线照射桌面后,在地面上形成阴影.已知桌面的直径为1.2 m,桌面距离地面1 m.若灯泡距离地面3 m,则地面上阴影部分的面积为 ( )

A. 0.36πm2 B. 0.81πm2 C. 2πm2 D. 3.24πm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边三角形网格中建立平面斜坐标系![]() ,对于其中的“格点
,对于其中的“格点![]() ”(落在网格线交点处的点),过点
”(落在网格线交点处的点),过点![]() 分别做
分别做![]() 轴,
轴, ![]() 轴的平行线,找到平行线与另一坐标轴的交点的
轴的平行线,找到平行线与另一坐标轴的交点的![]() 坐标和
坐标和![]() 坐标,记这个有序数对
坐标,记这个有序数对![]() 为它的坐标,如
为它的坐标,如![]() ,
,![]() ,规定当点在
,规定当点在![]() 轴上时,
轴上时,![]() 坐标为0,如
坐标为0,如![]() ;当点在
;当点在![]() 轴上时,
轴上时,![]() 坐标为0.
坐标为0.
(1)原点![]() 的坐标为 ,格点
的坐标为 ,格点![]() 的坐标为 .
的坐标为 .
(2)在图中画出点![]() ,
,![]() 的位置;
的位置;
(3)直线![]() 上的格点
上的格点![]() 的坐标满足的条件是 (其中
的坐标满足的条件是 (其中![]() 为整数).
为整数).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com