练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    7．已知一次函数y=kx+m-2x与y轴的负半轴相交，且函数值y随x增大而减小，则下列结论正确的是（　　）
    A．k＜2，m＞0B．k＜2，m＜0C．k＞2，m＞0D．k＞2，m＜0

    分析 依照题意画出函数图象，利用一次函数图象与系数的关系，即可得出关于k、m的一元一次不等式，解之即可得出结论．

    解答 解：依照题意画出函数图象，如图所示．
    ∵y=kx+m-2x=（k-2）x+m，
    ∴k-2＜0，m＜0，
    ∴k＜2，m＜0．
    故选B．

    点评 本题考查了一次函数图象与系数的关系，依照题意画出函数图象，利用函数图象找出k-2＜0、m＜0是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    17．下列方程组中，是二元一次方程组的是（　　）
    A．$\left\{\begin{array}{l}{x+y=5}\\{z+x=3}\end{array}\right.$B．$\left\{\begin{array}{l}{x+\frac{1}{y}=1}\\{\frac{1}{x}-y=3}\end{array}\right.$
    C．$\left\{\begin{array}{l}{x-y+xy=4}\\{3x-y=4}\end{array}\right.$D．$\left\{\begin{array}{l}{\frac{1}{2}x-2y=15}\\{\frac{1}{3}x+\frac{1}{2}y=4}\end{array}\right.$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．已知如图，直线y=kx+b与x轴、y轴分别交于点A、B，与直线y=3x交于点C，且|OA-6|+$\sqrt{OB-\frac{9}{2}}$=0，将直线y=kx+b沿直线y=3x折叠，与x轴交于点D，与y轴交于点E．
    （1）求直线y=kx+b的解析式及点C的坐标；
    （2）求△BCE的面积；
    （3）若点P是直线y=3x上的一个动点，在平面内是否存在一点Q，使以点A、C、P、Q为顶点的四边形是矩形？若存在，请直接写出点P、点Q的坐标；若不存在，请说明理由．

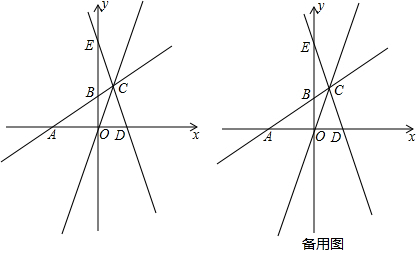
    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    15．某退休职工每天坚持体育锻炼，某天他慢步匀速到离家较远的和平广场，跳了一会儿广场坝坝舞后快步匀速回家，下面能反映当天他离家的路程y与时间x的函数关系的大致图象是（　　）
    A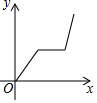．B．C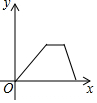．D．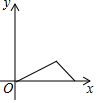

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．如图，下列三个条件：①AB∥CD，②∠B=∠C，③∠E=∠F．
    从中任选两个作为条件，另一个作为结论，共可编出几个真命题，并选一个加以证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．已知长方形纸片ABCD的长AD=8，宽AB=4，如图（1）．
    （1）将纸片沿EF折叠后，点D，C分别落在D′，C′的位置，如图（2）所示，若∠EFB=66°，求∠AED′的度数；
    （2）如图（3）所示，若点P从点C以2个单位长度/秒的速度在边CB上向点B移动，同时点Q从点B以1个单位长度/秒的速度在边BA上向点A移动，设移动的时间为t（0＜t＜4）秒，请问：在点P，Q移动的过程中，是否存在时间t的某一取值范围，使得S△ADQ＜S△DPC？若存在，求出时间t的取值范围；若不存在，说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．计算题：
    （1）（2x2）3-6x3（x3+2x2+x）；
    （2）（x+3）2-（x-1）（x-2）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

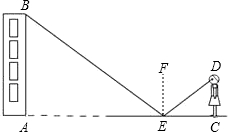    16．小玲用下面的方法来测量学校教学大楼AB的高度：如图，在水平面上放一面平面镜，镜子与教学楼的距离EA=12米，当她与镜子的距离CE=2米时，她刚好能从镜子中看到教学楼的顶端B．已知她的眼睛距地面的高度DC=1.5米．请你帮助小玲计算出教学楼的高度AB是多少米（根据光的反射定律：反射角等于入射角．）

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    17．下列四个命题是真命题的是（　　）
    A．内错角相等
    B．如果两个角的和是180°，那么这两个角是邻补角
    C．在同一平面内，平行于同一条直线的两条直线互相平行
    D．在同一平面内，垂直于同一条直线的两条直线互相垂直

    查看答案和解析>>

    同步练习册答案