
【题目】如图,矩形ABCD中,BC=2AB,对角线相交于O,过C点作CE⊥BD交BD于E点,H为BC中点,连接AH交BD于G点,交EC的延长线于F点,下列5个结论:①EH=AB;②∠ABG=∠HEC;③△ABG≌△HEC;④S△GAD=S四边形GHCE,⑤CF=BD.正确的有( )个.

A. 1 B. 2 C. 3 D. 4
【答案】C
【解析】
根据BC=2AB,H为BC中点,可得△ABH为等腰直角三角形,HE=BH=HC,可得△CEH为等腰三角形,又∠BCD=90°,CE⊥BD,利用互余关系得出角的相等关系,根据基本图形判断全等三角形,特殊三角形进行判断.
解:①在△BCE中,∵CE⊥BD,H为BC中点,
∴BC=2EH,又BC=2AB,
∴EH=AB,①正确;
②由①可知,BH=HE∴∠EBH=∠BEH,
又∠ABG+∠EBH=∠BEH+∠HEC=90°,
∴∠ABG=∠HEC,②正确;
③由AB=BH,∠ABH=90°,得∠BAG=45°,
同理:∠DHC=45°,∴∠EHC>∠DHC=45°,
∴△ABG≌△HEC,③错误;
④作AM⊥BD,则AM=CE,△AMD≌△CEB,
∵AD∥BC,
∴△ADG∽△HGB,
∴![]() =2,
=2,
即△ABG的面积等于△BGH的面积的2倍,
根据已知不能推出△AMG的面积等于△ABG的面积的一半,
即S△GAD≠S四边形GHCE,
∴④错误
⑤∠ECH=∠CHF+∠F=45°+∠F,
又∠ECH=∠CDE=∠BAO,∠BAO=∠BAH+∠HAC,
∴∠F=∠HAC,
∴CF=BD,⑤正确.
正确的有3个.
故选C.


科目:初中数学 来源: 题型:
【题目】问题提出:
(1)平面直角坐标系中,若点A(a,2a+1)在一次函数y=x-1的图像上,则a的值为___________;
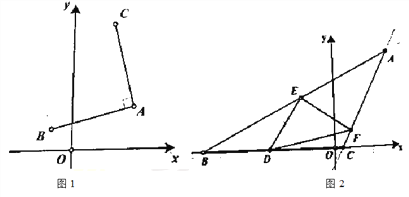
(2)如图1,平面直角坐标系中,已知A(4,2)、B(-1,1),若∠A=90°,点C在第一象限,且AB=AC,试求出C点坐标;
(3)近几年在经济、科技等多方面飞速发展的中国向世界展示了有一个繁华盛世.在政府的引导下,各地也都就本市特点修建了一些具有本地特色的旅游开发项目.如图2,某市就其地势特点,在一块由三条高速路(分别是x轴和直线AB:![]() 、直线AC:y=2x-1)围成的三角形区域内计划修建一个三角形的特色旅游小镇.如图,D(-4,0),△DEF的顶点E、F分别在线段AB、AC上,且∠DEF=90°,DE=EF,试求出该旅游小镇(△DEF)的面积.
、直线AC:y=2x-1)围成的三角形区域内计划修建一个三角形的特色旅游小镇.如图,D(-4,0),△DEF的顶点E、F分别在线段AB、AC上,且∠DEF=90°,DE=EF,试求出该旅游小镇(△DEF)的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某产品每件成本10元,试销阶段每件产品的销售单价x(元/件)与日销售量y(件)之间的关系如下表.
x(元∕件) | 15 | 18 | 20 | 22 | … |
y(件) | 250 | 220 | 200 | 180 | … |
按照这样的规律可得,日销售利润w(元)与销售单价x(元/件)之间的函数关系式是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,已知点![]() 是
是![]() 外一点,连接
外一点,连接![]() ,
,![]() .求
.求![]() 的度数.
的度数.
请补充下面的推理过程:
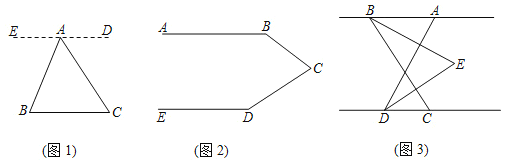
解:过点![]() 作
作![]() ,所以
,所以![]() ,
,![]() _______.
_______.
又因为![]() °,所以
°,所以![]() .
.
(2)如图2,已知![]() ,借鉴(1)的方法,求
,借鉴(1)的方法,求![]() 的度数;
的度数;
(3)如图3,已知![]() ,
,![]() .
.![]() ,
,![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,
,![]() ,
,![]() 所在的直线交于点
所在的直线交于点![]() ,点
,点![]() 在
在![]() 与
与![]() 两条平行线之间,借鉴(1)的方法,求
两条平行线之间,借鉴(1)的方法,求![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB、CD相交于点O,∠BOM=90°,∠DON=90°.
(1)若∠COM=∠AOC,求∠AOD的度数;
(2)若∠COM=![]() ∠BOC,求∠AOC和∠MOD.
∠BOC,求∠AOC和∠MOD.

查看答案和解析>>
科目:初中数学 来源: 题型:
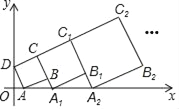
【题目】在平面直角坐标系中,正方形ABCD的位置如右图所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点A1,作正方形A1B1C1C;延长C1B1交x轴于点A2,作正方形A2B2C2C1,…按这样的规律进行下去,第2017个正方形的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的顶点坐标为A(1,2),B(2,3),C(4,1).

(1)在图中作出△ABC关于y轴对称的△A1B1C1,其中点A1的坐标为 ;
(2)将△A1B1C1向下平移4个单位得到△A2B2C2,请画出△A2B2C2,其中点B2的坐标为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com