
 长方形OABC绕顶点C(0,5)逆时针方向旋转,当旋转到CO′A′B′位置时,边O′A′交边AB于D,且A′D=2,AD=4.
长方形OABC绕顶点C(0,5)逆时针方向旋转,当旋转到CO′A′B′位置时,边O′A′交边AB于D,且A′D=2,AD=4.分析 (1)先根据旋转的性质以及矩形的性质,求得BC=AO=O′A′,AB=CO=CO'=5,∠B=∠O'=90°,BD=1,再连接CD,设BC=x,根据勾股定理得出BC2+BD2=CD2=CO'2+DO'2,据此列出方程求解即可;
(2)根据阴影部分的面积=△BCD面积+△O'CD面积,进行计算即可.
解答 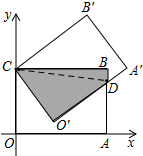 解:(1)∵长方形OABC绕顶点C(0,5)逆时针方向旋转得到矩形CO′A′B′
解:(1)∵长方形OABC绕顶点C(0,5)逆时针方向旋转得到矩形CO′A′B′
∴BC=AO=O′A′,AB=CO=CO'=5,∠B=∠O'=90°,
∵AD=4,AB=5,
∴BD=5-4=1,
设BC=x,则DO'=O'A'-A'D=x-2,
连接CD,则BC2+BD2=CD2=CO'2+DO'2
即x2+12=52+(x-2)2
解得:x=7,
∴BC=7;
(2)∵BC=7,BD=1,CO'=5,DO'=7-2=5,∠B=∠O'=90°,
∴阴影部分的面积=△BCD面积+△O'CD面积=$\frac{1}{2}$×7×1+$\frac{1}{2}$×5×5=16.
点评 本题主要考查了旋转的性质以及矩形的性质,解决问题的关键是连接CD,构造两个直角三角形,根据公共边相等,运用勾股定理列出方程.解题时注意方程思想的灵活运用.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题


查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com