
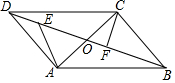
 如图,点O为?ABCD的对角线AC,BD的交点,∠BCO=90°,∠BOC=60°,BD=8,点E是OD上的一动点,点F是OB上的一动点(E,F不与端点重合),且DE=OF,连接AE,CF.
如图,点O为?ABCD的对角线AC,BD的交点,∠BCO=90°,∠BOC=60°,BD=8,点E是OD上的一动点,点F是OB上的一动点(E,F不与端点重合),且DE=OF,连接AE,CF.分析 (1)根据平行四边形的性质得到OD=OB,于是得到结论;
(2)如图所示,连结AF,由四边形ABCD是平行四边形,得到AO=OC,求得S△AOF=S△COF,于是得到S1+S2=S△AEF=S△AOD,即可得到结论;
(3)当DE=OE时,AE+CF的值最小,此时E为OD的中点,于是得到结论.
解答 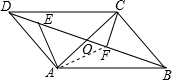 解:(1)∵四边形ABCD是平行四边形,
解:(1)∵四边形ABCD是平行四边形,
∴OD=OB,
∵DE=OF,
∴EF=OD=$\frac{1}{2}$BD=4;
(2)S1+S2的值不变,理由如下:
如图所示,连结AF,
∵四边形ABCD是平行四边形,
∴AO=OC,
∴S△AOF=S△COF,
∵DE=OF,
∴S△ADE=S△COF,
∴S1+S2=S△AEF=S△AOD,
∵∠BCO=90°,∠BOC=60°,
∴∠DAC=90°,∠AOD=60°,
∴AO=$\frac{1}{2}$OD=2,
在Rt△AOD中,AD=$\sqrt{3}$AO=2$\sqrt{3}$,
∴S1+S2=S△AOD=$\frac{1}{2}$AD•OA=$\frac{1}{2}$×2$\sqrt{3}$×2=2$\sqrt{3}$;
(3)当DE=OE时,AE+CF的值最小,此时E为OD的中点,
∵∠OAD=90°,
∴AE=$\frac{1}{2}$OD=2,
同理BQ=2,
∴AE+CF的最小值=4.
点评 本题是四边形综合题目,考查了平行四边形的性质、含30°角的直角三角形的性质、勾股定理、直角三角形斜边上的中线性质、三角形面积的计算等知识;本题难度较大,综合性强,特别是(2)(3)中,需要运用勾股定理、直角三角形斜边上的中线性质等知识才能得出结果.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,直线y=kx-1与x轴、y轴分别交于B、C两点,且3BO-$\frac{1}{2}$CO=1
如图,直线y=kx-1与x轴、y轴分别交于B、C两点,且3BO-$\frac{1}{2}$CO=1查看答案和解析>>
科目:初中数学 来源: 题型:填空题
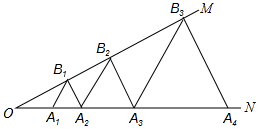 如图,∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,从左起第1个等边三角形的边长记为a1,第2个等边三角形的边长记为a2,以此类推.若OA1=1,则a2017=22016.
如图,∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,从左起第1个等边三角形的边长记为a1,第2个等边三角形的边长记为a2,以此类推.若OA1=1,则a2017=22016.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
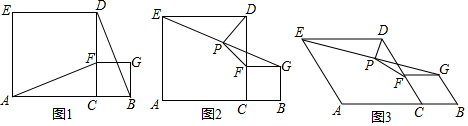
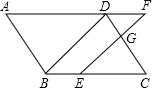 如图,在平行四边形ABCD中,点E在边BC上,点F在边AD的延长线上,且DF=BE,EF与CD交于点G.
如图,在平行四边形ABCD中,点E在边BC上,点F在边AD的延长线上,且DF=BE,EF与CD交于点G.查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | 22 | B. | 25 | C. | 47 | D. | 50 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com