
【题目】当m是何值时,关于x的方程(m2+2)x2+(m﹣1)x﹣4=3x2
(1)是一元二次方程;
(2)是一元一次方程;
(3)若x=﹣2是它的一个根,求m的值.
【答案】(1)m≠±1;(2)m=﹣1;(3)m1=![]() .
.
【解析】【试题分析】(m2+2)x2+(m﹣1)x﹣4=3x2,化为一般式得: ![]() ,
,
(1)根据一元二次方程的定义,要求二次项系数不能为0,即![]() ,解得m≠±1;
,解得m≠±1;
(2)根据一元一次方程的定义,要求二次项不存在,即二次项系数为0,且一次项系数不为0,即![]() ,解得:m=﹣1;
,解得:m=﹣1;
(3)根据方程的根的定义将x=﹣2代入![]() ,得:
,得: ![]() ,
, ![]() 解得:m1=
解得:m1=![]() ,m2=﹣1,又因为
,m2=﹣1,又因为![]() ,所以m=
,所以m=![]() .
.
【试题解析】
原方程可化为(m2﹣1)x2+(m﹣1)x﹣4=0,
(1)当m2﹣1≠0,即m≠±1时,是一元二次方程;
(2)当m2﹣1=0,且m﹣1≠0,即m=﹣1时,是一元一次方程;
(3)x=﹣2时,原方程化为:2m2﹣m﹣3=0,
解得,m1=![]() ,m2=﹣1(舍去).即m=
,m2=﹣1(舍去).即m=![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2-2x-m2=0.
(1)求证:该方程有两个不相等的实数根;
(2)若该方程有两个实数根为x1,x2,且x1=2x2+5,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为8,在各边上顺次截取AE=BF=CG=DH=5,则四边形EFGH的面积是( )

A. 30 B. 34 C. 36 D. 40
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A、B两地相距120千米,甲骑自行车以20千米/时的速度由起点A前往终点B,乙骑摩托车以40千米/时的速度由起点B前往终点A.两人同时出发,各自到达终点后停止.设两人之间的距离为s(千米),甲行驶的时间为t(小时),则下图中正确反映s与t之间函数关系的是( )
A. 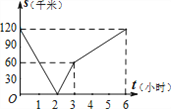 B.
B. 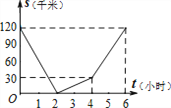
C.  D.
D. 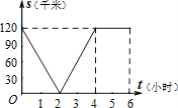
查看答案和解析>>
科目:初中数学 来源: 题型:
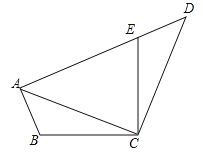
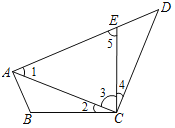
【题目】如图,已知在四边形ABCD中,点E在AD上,∠BCE=∠ACD=90°,∠BAC=∠D,BC=CE.
(1)求证:AC=CD;
(2)若AC=AE,求∠DEC的度数.
【答案】(1)证明见解析;(2)112.5°.
【解析】试题分析: ![]() 根据同角的余角相等可得到
根据同角的余角相等可得到![]() 结合条件
结合条件![]() ,再加上
,再加上![]() 可证得结论;
可证得结论;![]() 根据
根据![]() 得到
得到![]() 根据等腰三角形的性质得到
根据等腰三角形的性质得到![]() 由平角的定义得到
由平角的定义得到![]()
试题解析: ![]() 证明:
证明:
![]()
![]()
![]()
在△ABC和△DEC中,  ,
,
![]()
![]()
(2)∵∠ACD=90°,AC=CD,
∴∠1=∠D=45°,
∵AE=AC,
∴∠3=∠5=67.5°,
∴∠DEC=180°-∠5=112.5°.
【题型】解答题
【结束】
21
【题目】一个零件的形状如图所示,工人师傅按规定做得∠B=90°,
AB=3,BC=4,CD=12,AD=13,假如这是一块钢板,你能帮工人师傅计算一下这块钢板的面积吗?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在菱形ABCD中,F是BC上任意一点,连接AF交对角线BD于点E,连接EC.

(1)求证:AE=EC;
(2)当∠ABC=60°,∠CEF=60°时,点F在线段BC上的什么位置?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点G在对角线BD上(不与点B,D重合),GE⊥DC于点E,GF⊥BC于点F,连结AG.
(1)写出线段AG,GE,GF长度之间的数量关系,并说明理由;
(2)若正方形ABCD的边长为1,∠AGF=105°,求线段BG的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某旅行社组织一批游客外出旅游,原计划租用45座客车若干辆,但有15人没有座位;若租用同样数量的60座客车,则多出一辆车,且其余客车恰好坐满.已知45座客车租金为每辆220元,60座客车租金为每辆300元,问:
(1)这批游客的人数是多少?原计划租用多少辆45座客车?
(2)若租用同一种车,要使每位游客都有座位,应该怎样租用才合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB∥CD,CE,BE的交点为E,现作如下操作:
第一次操作,分别作∠ABE和∠DCE的平分线,交点为E1,
第二次操作,分别作∠ABE1和∠DCE1的平分线,交点为E2,
第三次操作,分别作∠ABE2和∠DCE2的平分线,交点为E3……
第n次操作,分别作∠ABEn-1和∠DCEn-1的平分线,交点为En.
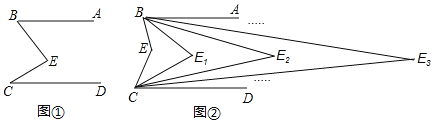
(1)如图①,求证:∠E=∠B+∠C;
(2)如图②,求证:∠E1=![]() ∠E;
∠E;
(3)猜想:若∠En=b°,求∠BEC的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com