
| 1 |
| 2 |
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案科目:初中数学 来源: 题型:
| ||
| 2 |
| AB |
| BC |
| ||
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
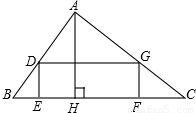
 如图,有一块直角三角形土地,它两条直角边AB=300米,AC=400米,某单位要沿着斜边BC修一座底面是矩形DEFG的大楼,D、G分别在边AB、AC上,设EF为x,矩形面积为y.
如图,有一块直角三角形土地,它两条直角边AB=300米,AC=400米,某单位要沿着斜边BC修一座底面是矩形DEFG的大楼,D、G分别在边AB、AC上,设EF为x,矩形面积为y.查看答案和解析>>
科目:初中数学 来源:2012年甘肃省中考数学仿真模拟试卷(解析版) 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 ,底角平分线与腰的交点为黄金分割点.
,底角平分线与腰的交点为黄金分割点. ,则请你求出∠A的度数;
,则请你求出∠A的度数;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com