
 在平面直角坐标xOy中,已知点A(6,0),点B(0,6),动点C在以半径为3的⊙O上,连接OC,过O点作OD⊥OC,OD与⊙O相交于点D(其中点C、O、D按逆时针方向排列),连接AB.
在平面直角坐标xOy中,已知点A(6,0),点B(0,6),动点C在以半径为3的⊙O上,连接OC,过O点作OD⊥OC,OD与⊙O相交于点D(其中点C、O、D按逆时针方向排列),连接AB.分析 (1)根据点A和点B坐标易得△OAB为等腰直角三角形,则∠OBA=45°,由于OC∥AB,所以当C点在y轴左侧时,有∠BOC=∠OBA=45°;当C点在y轴右侧时,有∠BOC=180°-∠OBA=135°,从而得出答案;
(2)由△OAB为等腰直角三角形得AB=$\sqrt{2}$OA,根据三角形面积公式得到当点C到AB的距离最大时,△ABC的面积最大,过O点作OE⊥AB于E,OE的反向延长线交⊙O于C,此时C点到AB的距离的最大值为CE的长,然后利用等腰直角三角形的性质计算出OE,然后计算△ABC的面积;
(3)由(2)可知当△ABC的面积最大值时,则点C在第三象限,因为OD⊥OC,所以点D在第二象限,过点D作DH⊥OB,DM⊥AO,分别求出DH,DM的长即可求出点D的坐标.
解答 解:(1)∵点A(6,0),点B(0,6),
∴OA=OB=6,
∴△OAB为等腰直角三角形,
∴∠OBA=45°,
∵OC∥AB,
∴当C点在y轴左侧时,∠BOC=∠OBA=45°,
当C点在y轴右侧时,∠BOC=180°-∠OBA=135°,
∴∠OBA=45°或135°;
故答案为:45°或135°;
(2)∵△OAB为等腰直角三角形,
∴AB=$\sqrt{2}$OA=6$\sqrt{2}$,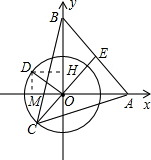
∴当点C到AB的距离最大时,△ABC的面积最大,
过O点作OE⊥AB于E,OE的反向延长线交⊙O于C,
如图:此时C点到AB的距离最大值为CE的长,
∵△OAB为等腰直角三角形,
∴OE=$\frac{1}{2}$AB=3$\sqrt{2}$,
∴CE=OC+OE=3+3$\sqrt{2}$,△ABC的面积=$\frac{1}{2}$CE•AB=$\frac{1}{2}$(3+3$\sqrt{2}$)×6$\sqrt{2}$=9$\sqrt{2}$+18,
当点C在⊙O上运动到第三象限的角平分线与圆的交点位置时,△ABC的面积最大,最大值为9$\sqrt{2}$+18.
(3)过点D作DH⊥OB,DM⊥AO,
由(2)可知点C在⊙O上运动到第三象限的角平分线与圆的交点位置,
∴∠COM=45°,
∵OD⊥OC,
∴∠DOM=45°,
∵OD=3,
∴DM=$\frac{3\sqrt{2}}{2}$,DH=$\frac{3\sqrt{2}}{2}$,
∴点D坐标是(-$\frac{3\sqrt{2}}{2}$,$\frac{3\sqrt{2}}{2}$).
点评 本题考查了圆的综合题,用到的知识点是平行线的性质和等腰直角三角形的判定与性质;熟练运用勾股定理进行几何计算是本题的关键.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:初中数学 来源: 题型:填空题
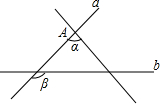 如图,直线a与直线c的夹角是∠α,直线b与直线c的夹角是∠β,把直线a“绕”点A按逆时针方向旋转,当∠α与∠β满足∠α=∠β时,直线a∥b,理由是同位角相等,两直线平行.
如图,直线a与直线c的夹角是∠α,直线b与直线c的夹角是∠β,把直线a“绕”点A按逆时针方向旋转,当∠α与∠β满足∠α=∠β时,直线a∥b,理由是同位角相等,两直线平行.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在△ABC中,点D是BC的中点,点E、F分别在线段AD及其延长线上,且DE=DF.下列条件使四边形BECF为菱形的是( )
如图,在△ABC中,点D是BC的中点,点E、F分别在线段AD及其延长线上,且DE=DF.下列条件使四边形BECF为菱形的是( )| A. | BE⊥CE | B. | BF∥CE | C. | BE=CF | D. | AB=AC |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在菱形ABCD中,∠B=60°,AB=2,扇形AEF的半径为2,圆心角为60°,则阴影部分的面积是$\frac{2}{3}π$-$\sqrt{3}$.
如图,在菱形ABCD中,∠B=60°,AB=2,扇形AEF的半径为2,圆心角为60°,则阴影部分的面积是$\frac{2}{3}π$-$\sqrt{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com