
分析 在直角△ABC中,根据AB、∠ACB可以求得BC的长度,在直角△ADB中,根据AB、∠BAD可以求得BD的长度,根据CD=CB-BD可以求得CD的长度,即可解题.
解答  解:根据题意得:∠C=∠EAC=15°,∠ADB=∠EAD=75°,
解:根据题意得:∠C=∠EAC=15°,∠ADB=∠EAD=75°,
∴∠DAB=15°,
在Rt△ABD中,tan∠DAB=$\frac{BD}{AB}$,
∵tan15°=2-$\sqrt{3}$,
∴BD=AB•tan15°=400-200$\sqrt{3}$,
在Rt△ABc中,tan∠ACB=tan15°=$\frac{AB}{BC}$,
∴BC=$\frac{200}{2-\sqrt{3}}$=400+200$\sqrt{3}$,
∴CD=BC-BD=400$\sqrt{3}$,
∴两船间的距离是400$\sqrt{3}$.
故答案为:400$\sqrt{3}$.
点评 本题考查了解直角三角形的应用-俯角和仰角问题,本题中计算BC、BD的值是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 1.05cm | B. | 0.525cm | C. | 4.2cm | D. | 2.1cm |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在矩形ABCD中,AB=5,BC=13,以B为圆心BC为半径画弧交AD于点E,连接CE,作BF⊥CE,垂足为F,则cos∠FBC的值为$\frac{5\sqrt{26}}{26}$.
如图,在矩形ABCD中,AB=5,BC=13,以B为圆心BC为半径画弧交AD于点E,连接CE,作BF⊥CE,垂足为F,则cos∠FBC的值为$\frac{5\sqrt{26}}{26}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知反比例函数y=$\frac{k}{x}$(x>0,k是常数)的图象经过点A(1,5),点B(m,n),其中m>1,AM⊥x轴,垂足为M,BN⊥y轴,垂足为N,AM与BN的交点为C.
如图,已知反比例函数y=$\frac{k}{x}$(x>0,k是常数)的图象经过点A(1,5),点B(m,n),其中m>1,AM⊥x轴,垂足为M,BN⊥y轴,垂足为N,AM与BN的交点为C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
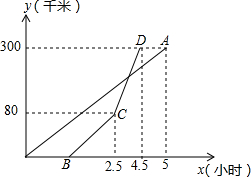 甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发向乙地.如图,线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数关系式;折线B-C-D表示轿车离甲地距离y(千米)与x(小时)之间的函数关系.下列四种说法:
甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发向乙地.如图,线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数关系式;折线B-C-D表示轿车离甲地距离y(千米)与x(小时)之间的函数关系.下列四种说法:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com