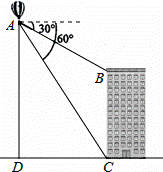
热气球的探测器显示，从热气球底部A处看一栋高楼顶部的俯角为30°，看这栋楼底部的俯角为60°，热气球A处于地面距离为420米，求这栋楼的高度．
一线名师权威作业本系列答案科目：初中数学 来源： 题型：
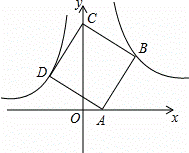
如图，点B（3，3）在双曲线y=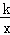
（x＞0）上，点D在双曲线y=﹣
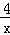（x＜0）上，点A和点C分别在x轴，y轴的正半轴上，且点A，B，C，D构成的四边形为正方形．
（1）求k的值；
（2）求点A的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
把三张形状、大小相同但画面不同的风景图片，都按同样的方式剪成相同的两片，然后堆放到一起混合洗匀，从这堆图片中随机抽出两张，这两张图片恰好能组成一张原风景图片的概率是
查看答案和解析>>
科目：初中数学 来源： 题型：
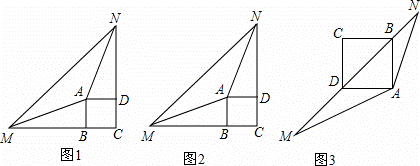
已知∠MAN=135°，正方形ABCD绕点A旋转．
（1）当正方形ABCD旋转到∠MAN的外部（顶点A除外）时，AM，AN分别与正方形ABCD的边CB，CD的延长线交于点M，N，连接MN．
①如图1，若BM=DN，则线段MN与BM+DN之间的数量关系是 MN=BM+DN ；
②如图2，若BM≠DN，请判断①中的数量关系是否仍成立？若成立，请给予证明；若不成立，请说明理由；
（2）如图3，当正方形ABCD旋转到∠MAN的内部（顶点A除外）时，AM，AN分别与直线BD交于点M，N，探究：以线段BM，MN，DN的长度为三边长的三角形是何种三角形，并说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
下列说法正确的是（ ）
A．面积相等的两个三角形全等
B．矩形的四条边一定相等
C．一个图形和它旋转后所得图形的对应线段相
D．随机投掷一枚质地均匀的硬币，落地后一定是正面朝上等
查看答案和解析>>
科目：初中数学 来源： 题型：
某公司生产的某种产
品每件成本为40元，经市场调查整理出如下信息：
①该产品90天内日销售量（m件）与时间（第x天）满足一次函数关系，部分数据如下表：
| 时间（第x天） | 1 | 3 | 6 | 10 | … |
| 日销售量（m件） | 198 | 194 |
| 180 | … |
②该产品90天内每天的销售价格与时间（第x天）的关系如下表：
| 时间（第x天） | 1≤x＜50 | 50≤x≤90 |
| 销售价格（元/件） | x+60 | 100 |
（1）求m关于x的一次函数表达式；
（2）设销售该产品每天利润为y元，请写出y关于x的函数表达式，并求出在90天内该产品哪天的销售利润最大？最大利润是多少？【提示：每天销售利润=日销售量×（每件销售价格-每件成本）】
（3）在该产品销售的过程中，共有多少天销售利润不低于5400元，请直接写出结果．
查看答案和解析>>
科目：初中数学 来源： 题型：
如图,在边长为6的正方形ABCD中,E是AB的中点,以E为圆心,ED为半径作半圆,交A、B所在的直线于M、N两点,分别以直径MD、ND
为直径作半圆,则阴影部分面积为( )
|
|
| 第12题 |
A.9
B.18 C.36 D.72
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
=140
（米），
米．
=140（米），
+（11﹣1）0﹣4×
．
+
=
÷
=3