
����Ŀ����ƽ��ֱ������ϵ�У���֪�����߾���A����4��0����B��0����4����C��2��0�����㣮
��1���������߽���ʽ��
��2������MΪ������������������һ���㣬��M�ĺ�����Ϊm����MOA�����ΪS����S����m�ĺ�����ϵʽ���������mΪ��ֵʱ��S�����ֵ��������ֵ�Ƕ��٣�
��3������Q��ֱ��y=��x�ϵĶ��㣬��Q��y���ƽ���߽��������ڵ�P���ж��м���Q��ʹ�Ե�P��Q��B��OΪ������ı�����ƽ���ı��εĵ㣬ֱ��д����Ӧ�ĵ�Q�����꣮

���𰸡���1��y=![]() x2+x��4����2��S����m�ĺ�����ϵʽΪS=��m2��2m+8����m=��1ʱ��S�����ֵ9����3��Q����Ϊ����4��4����2+2
x2+x��4����2��S����m�ĺ�����ϵʽΪS=��m2��2m+8����m=��1ʱ��S�����ֵ9����3��Q����Ϊ����4��4����2+2![]() ��2��2
��2��2![]() ����2��2
����2��2![]() ��2+2
��2+2![]() ��ʱ��ʹ��P��Q��B��OΪ������ı�����ƽ���ı��Σ�
��ʱ��ʹ��P��Q��B��OΪ������ı�����ƽ���ı��Σ�
��������
(1)�������߽���ʽΪy�� ax2 �� bx �� c,Ȼ��ѵ�A��B��C��������뺯������ʽ�����ô���ϵ������⼴��;
(2)���������ߵĽ���ʽ��ʾ����M�������꣬�Ӷ��õ���M��x��ľ��룬Ȼ����������������ʽ��ʾ���������ɵý⣬���������ߵ�����������������ڶ��κ�������ֵ��Ȼ�ɵý�;
(3)����ֱ���������ߵĽ���ʽ��ʾ����P��Q�����꣬Ȼ�����PQ�ij��ȣ��ٸ���ƽ���ı��εĶԱ�����г���ʽ��Ȼ������x��һԪ���η��̼��ɵý�.
�⣺��1���������߽���ʽΪy=ax2+bx+c��
�������߾���A����4��0����B��0����4����C��2��0����
��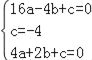 ��
��
���![]() ��
��
�������߽���ʽΪy=![]() x2+x��4��
x2+x��4��
��2������M�ĺ�����Ϊm��
����M��������Ϊ![]() m2+m��4��
m2+m��4��
����A����4��0����
��AO=0������4��=4��
��S=![]() ��4��|
��4��|![]() m2+m��4|=����m2+2m��8��=��m2��2m+8��
m2+m��4|=����m2+2m��8��=��m2��2m+8��
��S=����m2+2m��8��=����m+1��2+9����MΪ������������������һ���㣬
����m=��1ʱ��S�����ֵ�����ֵΪS=9��
�ʴ�Ϊ��S����m�ĺ�����ϵʽΪS=��m2��2m+8����m=��1ʱ��S�����ֵ9��
��3������Q��ֱ��y=��x�ϵĶ��㣬
�����Q��������a����a����
����P���������ϣ���PQ��y�ᣬ
����P��������a��![]() a2+a��4����
a2+a��4����
��PQ=��a����![]() a2+a��4��=��
a2+a��4��=��![]() a2��2a+4��
a2��2a+4��
����OB=0������4��=4��
�Ե�P��Q��B��OΪ������ı�����ƽ���ı��Σ�
��|PQ|=OB��
��|��![]() a2��2a+4|=4��
a2��2a+4|=4��
�٩�![]() a2��2a+4=4ʱ�������ã�a2+4a=0��
a2��2a+4=4ʱ�������ã�a2+4a=0��
���a=0����ȥ����a=��4��
��a=4��
���Ե�Q����Ϊ����4��4����
�ک�![]() a2��2a+4=��4ʱ�������ã�a2+4a��16=0��
a2��2a+4=��4ʱ�������ã�a2+4a��16=0��
���a=��2��2![]() ��
��
���Ե�Q������Ϊ����2+2![]() ��2��2
��2��2![]() ����2��2
����2��2![]() ��2+2
��2+2![]() ����
����
����������Q��������4��4����2+2![]() ��2��2
��2��2![]() ����2��2
����2��2![]() ��2+2
��2+2![]() ��ʱ��ʹ��P��Q��B��OΪ������ı�����ƽ���ı��Σ�
��ʱ��ʹ��P��Q��B��OΪ������ı�����ƽ���ı��Σ�


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������������У������е�ÿ��С�����α߳���1������ABC�Ķ�����ڸ���ϣ�����������ֱ������ϵ�н���������⣺

��1����������ABC��AΪ��ת���ģ���˳ʱ�뷽����ת90�����ͼ����AB1C1����B1������Ϊ ��
��2������ABC����ԭ��O�����ĶԳƵġ�A2B2C2����B2������Ϊ .
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У���ACB��90����DΪAB��һ�㣬��D����AB���ߣ���AC��E����BC���ӳ�����F��

��1����1���B��ʲô��ϵ��˵�����ɣ�
��2����BC��BD������̽��AB��FB��������ϵ������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ -3��-1��0��1��3��������������ȡһ������Ϊa���ٴ�ʣ�µ��ĸ����������ȡһ������Ϊb��ǡ��ʹ����x��y�Ķ�Ԫһ�η�����![]() �������⣬�ҵ�(a��b)����˫����
�������⣬�ҵ�(a��b)����˫����![]() �ϵĸ�����_________.
�ϵĸ�����_________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽�һ�����ƻ���,֣���н�����������ɫ���г�������,��֪A�ͺŵ����г���B�ͺŵ����г��ĵ��۵�30Ԫ,��8��A�ͺŵ����г�����7��B�ͺŵ����г�����������ͬ.
(1)A,B�����ͺŵ����г��ĵ��۷ֱ��Ƕ���?
(2)������A,B�������г���600��,��A�ͺ����г�������������B�ͺ����г���һ��,�������һ����ʡǮ�ķ���,������÷�������Ҫ�ķ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ�����Ӧ��
����ϵ��������ijһ����ʽ��ȫ����ϵ��Ϊδ֪�������õ���������ʽΪ���ʽʱ��ͬ����ϵ����ȵ�ԭ��ȷ����Щϵ�����Ӷ��õ������ֵ��
����ϵ��������Ӧ�õ���ʽ�ֽ��У��������⣺��ʽ�ֽ�![]() ��
��
��Ϊ![]() Ϊ���ζ���ʽ��������ʽ�ֽ⣬����Էֽ��һ��һ�ζ���ʽ��һ�����ζ���ʽ�ij˻���
Ϊ���ζ���ʽ��������ʽ�ֽ⣬����Էֽ��һ��һ�ζ���ʽ��һ�����ζ���ʽ�ij˻���
�����ǿ��Բ���![]() ���Էֽ��
���Էֽ��![]() ��չ����ʽ�ұߵã�
��չ����ʽ�ұߵã�
![]() �����ݴ���ϵ����ԭ������ʽ���߶���ʽ��ͬ����Ķ�Ӧϵ����ȣ�
�����ݴ���ϵ����ԭ������ʽ���߶���ʽ��ͬ����Ķ�Ӧϵ����ȣ�![]() ��
��![]() ��
��![]() �������
�������![]() ��
��![]() ��
��
����![]() ��
��
��1����![]() ȡ����ֵ����ʽ
ȡ����ֵ����ʽ![]() ���������
���������![]() ________��
________��
��2����֪����ʽ![]() ����ʽ
����ʽ![]() �����ô���ϵ��������ö���ʽ����һ��ʽ��
�����ô���ϵ��������ö���ʽ����һ��ʽ��
��3�����ж϶���ʽ![]() �Ƿ��ֽܷ�ɵ�������Ϊ��ϵ�����ζ���ʽ�ij˻�����˵�����ɣ�
�Ƿ��ֽܷ�ɵ�������Ϊ��ϵ�����ζ���ʽ�ij˻�����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������ABCD�У���MAN=45�㣬��MAN�Ƶ�A˳ʱ����ת���������߷ֱ�CB��DC�������ǵ��ӳ��ߣ��ڵ�M��N��AH��MN�ڵ�H��
��1������MAN�Ƶ�A��ת��BM=DNʱ������ֱ��д���߶�AH��AB��������ϵ______��������֤����
��2������MAN�Ƶ�A��ת��BM��DNʱ���ʣ�1�����߶�AH��AB��������ϵ��������������������֤��������������˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() �ķ���
�ķ���![]() ��
��
![]() ��֤������
��֤������![]() ȡ�κ�ʵ��ʱ����������ʵ������
ȡ�κ�ʵ��ʱ����������ʵ������
![]() ��������
��������![]() ��
��![]() Ϊ��������ͼ����
Ϊ��������ͼ����![]() ����������ĺ������Ϊ��������������ߵĽ���ʽ��
����������ĺ������Ϊ��������������ߵĽ���ʽ��
![]() ��֪������
��֪������![]() ������㣬����������꣮
������㣬����������꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���ABCD�У�AB=CD��BD�ǶԽ��ߣ��ֱ����A��C��AE��BD�ڵ�E��CF��BD�ڵ�F����AE=CF

��1����֤��AB��CD
��2����E��BF�е㣬�ҡ�ABE�����Ϊ1�����ı���ABCD�����Ϊ________.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com