
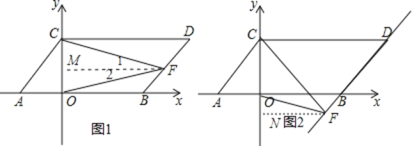
【题目】如图,在平面直角坐标系中,点![]() 的坐标分别是
的坐标分别是![]() ,现同时将点
,现同时将点![]() 分别向上平移2个单位长度,再向右平移2个单位长度,得到
分别向上平移2个单位长度,再向右平移2个单位长度,得到![]() 的对应点
的对应点![]() .连接
.连接![]() .
.
(1)写出点![]() 的坐标并求出四边形
的坐标并求出四边形![]() 的面积.
的面积.
(2)在![]() 轴上是否存在一点
轴上是否存在一点![]() ,使得
,使得![]() 的面积是
的面积是![]() 面积的2倍?若存在,请求出点
面积的2倍?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
(3)若点![]() 是直线
是直线![]() 上一个动点,连接
上一个动点,连接![]() ,当点
,当点![]() 在直线
在直线![]() 上运动时,请直接写出
上运动时,请直接写出![]() 与
与![]() 的数量关系.
的数量关系.

【答案】(1)点![]()
![]() ,点
,点![]()
![]() ;12;(2)存在,点
;12;(2)存在,点![]() 的坐标为
的坐标为![]() 和
和![]() ;(3) ∠OFC=∠FOB-∠FCD,见解析.
;(3) ∠OFC=∠FOB-∠FCD,见解析.
【解析】
(1)根据点平移的规律易得点C的坐标为(0,2),点D的坐标为(6,2);
(2)设点E的坐标为(x,0),根据△DEC的面积是△DEB面积的2倍和三角形面积公式得到![]() ,解得x=1或x=7,然后写出点E的坐标;
,解得x=1或x=7,然后写出点E的坐标;
(3)分类讨论:当点F在线段BD上,作FM∥AB,根据平行线的性质由MF∥AB得∠2=∠FOB,由CD∥AB得到CD∥MF,则∠1=∠FCD,所以∠OFC=∠FOB+∠FCD;同样得到当点F在线段DB的延长线上,∠OFC=∠FCD-∠FOB;当点F在线段BD的延长线上,得到∠OFC=∠FOB-∠FCD.
解:(1)∵点A,B的坐标分别是(-2,0),(4,0),现同时将点A、B分别向上平移2个单位长度,再向右平移2个单位长度得到A,B的对应点C,D,
∴点C的坐标为(0,2),点D的坐标为(6,2);
四边形ABDC的面积=2×(4+2)=12;
(2)存在.
设点E的坐标为(x,0),
∵△DEC的面积是△DEB面积的2倍,
![]() ,解得x=1或x=7,
,解得x=1或x=7,
∴点E的坐标为(1,0)和(7,0);
(3)当点F在线段BD上,作FM∥AB,如图1,
∵MF∥AB,
∴∠2=∠FOB,
∵CD∥AB,
∴CD∥MF,
∴∠1=∠FCD,
∴∠OFC=∠1+∠2=∠FOB+∠FCD;
当点F在线段DB的延长线上,作FN∥AB,如图2,
∵FN∥AB,
∴∠NFO=∠FOB,
∵CD∥AB,
∴CD∥FN,
∴∠NFC=∠FCD,
∴∠OFC=∠NFC-∠NFO=∠FCD-∠FOB;
同样得到当点F在线段BD的延长线上,得到∠OFC=∠FOB-∠FCD.


科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象分别与反比例函数y= ![]() 的图象在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB.
的图象在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB.
(1)求函数y=kx+b和y= ![]() 的表达式;
的表达式;
(2)已知点C(0,5),试在该一次函数图象上确定一点M,使得MB=MC,求此时点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算题( ![]() )﹣1+
)﹣1+ ![]() +sin30°;
+sin30°;
(1)计算:( ![]() )﹣1+
)﹣1+ ![]() +sin30°;
+sin30°;
(2)先化简,再求值:(m+2)(m﹣2)﹣(m﹣2)2+1,其中m=2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】科技馆是少年儿童节假日游玩的乐园.
如图所示,图中点的横坐标x表示科技馆从8:30开门后经过的时间(分钟),纵坐标y表示到达科技馆的总人数.图中曲线对应的函数解析式为y= ![]() ,10:00之后来的游客较少可忽略不计.
,10:00之后来的游客较少可忽略不计.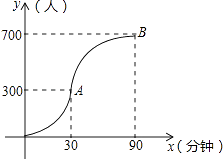
(1)请写出图中曲线对应的函数解析式;
(2)为保证科技馆内游客的游玩质量,馆内人数不超过684人,后来的人在馆外休息区等待.从10:30开始到12:00馆内陆续有人离馆,平均每分钟离馆4人,直到馆内人数减少到624人时,馆外等待的游客可全部进入.请问馆外游客最多等待多少分钟?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的周长为19,点D,E在边BC上,∠ABC的平分线垂直于AE,垂足为N,∠ACB的平分线垂直于AD,垂足为M,若BC=7,则MN的长度为( )

A. ![]() B. 2 C.
B. 2 C. ![]() D. 3
D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校准备购买若干台A型电脑和B型打印机.如果购买1台A型电脑,2台B型打印机,一共需要花费5900元;如果购买2台A型电脑,2台B型打印机,一共需要花费9400元.
(1)求每台A型电脑和每台B型打印机的价格分别是多少元?
(2)如果学校购买A型电脑和B型打印机的预算费用不超过20000元,并且购买B型打印机的台数要比购买A型电脑的台数多1台,那么该学校至多能购买多少台B型打印机?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一个有45°角的三角板的直角顶点放在一张宽为3cm的纸带边沿上,另一个顶
点在纸带的另一边沿上,测得三角板的一边与纸带的一边所在的直线成30°角,如图(3),
则三角板的最大边的长为( )
A. ![]() B.
B. ![]() C.
C.![]()
![]() D.
D. ![]()
![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠BAD=∠CAE=90°,AB=AD,AE=AC,AF⊥CB,垂足为F.
(1)求证:△ABC≌△ADE;
(2)求∠FAE的度数;
(3)求证:CD=2BF+DE.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图将小球从斜坡的O点抛出,小球的抛出路线可以用二次函数y=ax2+bx刻画,顶点坐标为(4,8),斜坡可以用 ![]() 刻画.
刻画.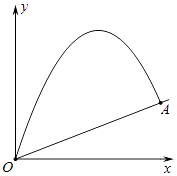
(1)求二次函数解析式;
(2)若小球的落点是A,求点A的坐标;
(3)求小球飞行过程中离坡面的最大高度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com