
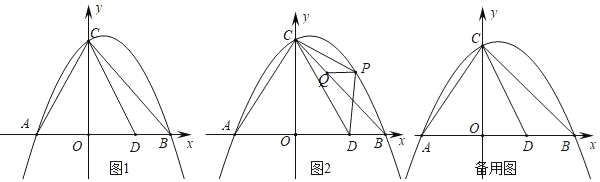
【题目】如图1,抛物线与y=﹣![]() 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,连接AC、BC,点D是线段AB上一点,且AD=CA,连接CD.
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,连接AC、BC,点D是线段AB上一点,且AD=CA,连接CD.
(1)如图2,点P是直线BC上方抛物线上的一动点,在线段BC上有一动点Q,连接PC、PD、PQ,当△PCD面积最大时,求PQ+![]() CQ的最小值;
CQ的最小值;
(2)将过点D的直线绕点D旋转,设旋转中的直线l分别与直线AC、直线CO交于点M、N,当△CMN为等腰三角形时,直接写出CM的长.
【答案】(1)![]() ;(2)CM的长为
;(2)CM的长为![]() 或
或![]() 或
或![]() .
.
【解析】
(1)设点P坐标,表示出△PCD的面积,列出二次函数关系式,求出△PCD面积最大时的点P坐标,作PG⊥CD,PG即为PQ+![]() CQ;
CQ;
(2)等腰三角形分类讨论,分别以C、N和M为等腰顶点分别讨论,求出此时的点M坐标,获得CM线段长.
解:(1)当y=0时,![]() ,
,
解得:x1=﹣3,x2=4,
∴A(﹣3,0),B(4,0),
∵x=0时,y=4,
∴C (0,4),
设OD=m,则AD=m+3,
在Rt△AOC中,有AC2=AO2+OC2,
∴(m+3)2=32+42,
解得:m1=2,m=2﹣8
∴D(2,0),
如图1,设点P(m,n),
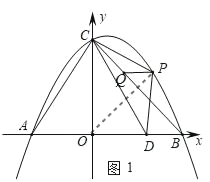
S△PCD=S△PCO+S△POD﹣S△COD
=![]()
=![]()
=![]()
=![]() ;
;
∵a=﹣![]() <0,则面积有最大值,
<0,则面积有最大值,
∴m=![]() 时,有最大值,
时,有最大值,
∴P(![]() ,
,![]() );
);
如图2,过点D作DH⊥CB,△DHB为等腰直角三角形,则DB=2,
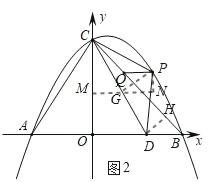
∴DH=BH=![]() ,
,
∵BC=![]() ,
,
∴CH=![]() ,
,
∴tan∠DCH=![]() .
.
过点P作PG⊥CD交BC于Q,则PG=PQ+![]() CQ,
CQ,
∴CD直线解析式为:y=﹣2x+4;
设G(m,﹣2m+4),
作GM⊥CO,PN⊥GM,垂足分别为M、N,可知△CMG∽△PGN,
∴![]() ,
,
∴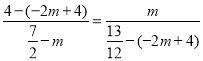 ,
,
解得:![]() ,
,
∵△CDO∽△GPN,
∴![]() ,
,
∴GP=![]() ,
,
∴PQ+![]() CQ的最小值为
CQ的最小值为![]() ;
;
(2)如图3,过点M1作M1H⊥AB,
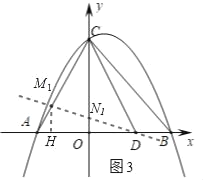
设直线L解析式为y=kx+b,
将(2,0)代入得:b=﹣2k,
∴y=kx﹣2k
①当CM1=CN1
∴ON1=﹣2k,CN1=4+2k,AM1=1﹣2k
∵△AM1H∽△AOC
∴![]() ,
,
∴![]() ,
,
∴AH=![]() (1﹣2k),M1H=
(1﹣2k),M1H=![]() ,
,
∴M1(![]() ,
,![]() ),
),
代入y=kx﹣2k得
![]() =k(
=k(![]() )﹣2k
)﹣2k
解得k1=﹣2,k2=![]() ,
,
∴CM=4+2k=![]() ;
;
②当CN2=MN2时,如图4
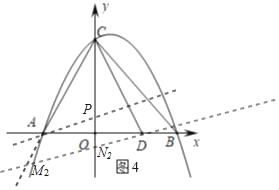
过A作AP∥BD,设AP直线解析式为y=kx+b,
将点A代入,﹣3k+b=0,
∴b=3k,
∴AP=![]() =
=![]() ,
,
∴CO=![]() +3k=4
+3k=4
∴k=![]() ,
,
∴DM直线解析式为:![]() ,
,
联立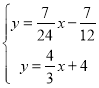 ,解得
,解得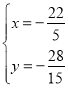
∴CM=![]() ;
;
③当M3C=M3N3时,如图5:
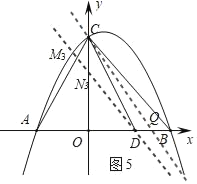
在x正半轴上取点Q(3,0),
∴CQ解析式为![]() ,
,
过点D作DM3∥CQ,
∴DM3的解析式为![]() ,
,
联立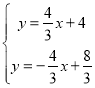 ,
,
解得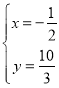 ,
,
∴M3(![]() ,
,![]() ),
),
∴CM3=![]() ;
;
综上所述:CM的长为:![]() 或
或![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】抛物线![]() 上部分点的横坐标
上部分点的横坐标![]() ,纵坐标
,纵坐标![]() 的对应值如下表:
的对应值如下表:
![]()
小聪观察上表,得出下面结论:①抛物线与x轴的一个交点为(3,0); ②函数![]() 的最大值为6;③抛物线的对称轴是
的最大值为6;③抛物线的对称轴是![]() ;④在对称轴左侧,y随x增大而增大.其中正确有( )
;④在对称轴左侧,y随x增大而增大.其中正确有( )
A. ①②B. ①③C. ①②③D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,函数
中,函数![]() 的图象经过点
的图象经过点![]() ,直线
,直线![]() 与x轴交于点
与x轴交于点![]() .
.
(1)求![]() 的值;
的值;
(2)过第二象限的点![]() 作平行于x轴的直线,交直线
作平行于x轴的直线,交直线![]() 于点C,交函数
于点C,交函数![]() 的图象于点D.
的图象于点D.
①当![]() 时,判断线段PD与PC的数量关系,并说明理由;
时,判断线段PD与PC的数量关系,并说明理由;
②若![]() ,结合函数的图象,直接写出n的取值范围.
,结合函数的图象,直接写出n的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某品牌牛奶供应商提供A,B,C,D四种不同口味的牛奶供学生饮用.某校为了了解学生对不同口味的牛奶的喜好,对全校订牛奶的学生进行了随机调查,并根据调查结果绘制了如下两幅不完整的统计图.根据统计图的信息解决下列问题:

(1)本次调查的学生有多少人?
(2)补全上面的条形统计图;
(3)扇形统计图中C对应的中心角度数是_____;
(4)若该校有600名学生订了该品牌的牛奶,每名学生每天只订一盒牛奶,要使学生能喝到自己喜欢的牛奶,则该牛奶供应商送往该校的牛奶中,A,B口味的牛奶共约多少盒?
查看答案和解析>>
科目:初中数学 来源: 题型:
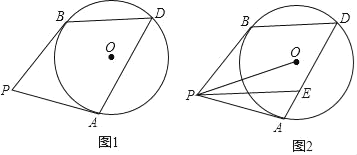
【题目】如图,PA、PB是⊙O的切线,A,B为切点,D为⊙O上一点.
(1)求证:∠P=180°﹣2∠D;
(2)如图,PE∥BD交AD于点E,若DE=2AE,tan∠OPE=![]() ,⊙O的半径为2
,⊙O的半径为2![]() ,求AE的长.
,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=x+2与抛物线y=ax2+bx+6(a≠0)相交于A(![]() )和B(4,6),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.
)和B(4,6),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.
(1)求抛物线的解析式;
(2)当C为抛物线顶点的时候,求![]() 的面积.
的面积.
(3)是否存在质疑的点P,使![]() 的面积有最大值,若存在,求出这个最大值,若不存在,请说明理由.
的面积有最大值,若存在,求出这个最大值,若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+3与x轴交于A(﹣1,0)和B(3,0)两点,与y轴交于点C,点D是该抛物线的顶点,分别连接AC、CD、AD.
(1)求抛物线的函数解析式以及顶点D的坐标;
(2)在抛物线上取一点P(不与点C重合)、并分别连接PA、PD,当△PAD的面积与△ACD的面积相等时,求点P的坐标:
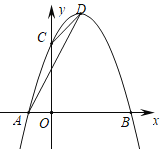
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,BC=![]() +
+![]() ,点D为边AB上一点,连接CD.将△ACD沿直线CD翻折至△ECD,CE恰好过AB的中点F.连接AE交CD的延长线于点H,若∠ACD=15°,则DH的长为( )
,点D为边AB上一点,连接CD.将△ACD沿直线CD翻折至△ECD,CE恰好过AB的中点F.连接AE交CD的延长线于点H,若∠ACD=15°,则DH的长为( )
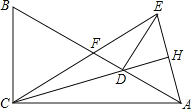
A.![]() B.
B.![]() C.
C.![]() D.1
D.1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com