Question

【题目】完成下面的证明（在括号中填写推理理由） 如图，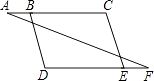

已知∠A=∠F，∠C=∠D，求证：BD∥CE．
证明：因为∠A=∠F，
所以AC∥DF（），
所以∠C+∠=180°（）．
因为∠C=∠D，
所以∠D+∠=180°（），
所以BD∥CE（）．

Answer 1

【答案】内错角相等，两直线平行；CED；两直线平行，同旁内角互补；CED；等量代换；同旁内角互补，两直线平行
【解析】证明：∵∠A=∠F， ∴AC∥DF（内错角相等，两直线平行），
∴∠C+∠CED=180°（两直线平行，同旁内角互补）．
∵∠C=∠D，
∴∠D+∠CDE=180°（等量代换），
∴BD∥CE（同旁内角互补，两直线平行），
所以答案是：内错角相等，两直线平行，CED，两直线平行，同旁内角互补，CED，等量代换，同旁内角互补，两直线平行．
【考点精析】解答此题的关键在于理解平行线的判定与性质的相关知识，掌握由角的相等或互补（数量关系）的条件，得到两条直线平行（位置关系）这是平行线的判定；由平行线（位置关系）得到有关角相等或互补（数量关系）的结论是平行线的性质．