
【题目】如图1是小明制作的一副弓箭,点A,D分别是弓臂BAC与弓弦BC的中点,弓弦BC=60cm.沿AD方向拉弓的过程中,假设弓臂BAC始终保持圆弧形,弓弦不伸长.如图2,当弓箭从自然状态的点D拉到点D1时,有AD1=30cm,∠B1D1C1=120°.
(1)图2中,弓臂两端B1,C1的距离为_____cm.
(2)如图3,将弓箭继续拉到点D2,使弓臂B2AC2为半圆,则D1D2的长为_____cm.

【答案】 30![]() 10
10![]() ﹣10,
﹣10,
【解析】(1)如图1中,连接B1C1交DD1于H.解直角三角形求出B1H,再根据垂径定理即可解决问题;
(2)如图3中,连接B1C1交DD1于H,连接B2C2交DD2于G.利用弧长公式求出半圆半径即可解决问题;
(1)如图2中,连接B1C1交DD1于H.
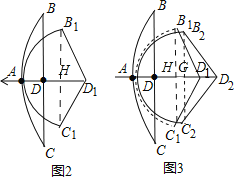
∵D1A=D1B1=30
∴D1是![]() 的圆心,
的圆心,
∵AD1⊥B1C1,
∴B1H=C1H=30×sin60°=15![]() ,
,
∴B1C1=30![]()
∴弓臂两端B1,C1的距离为30![]()
(2)如图3中,连接B1C1交DD1于H,连接B2C2交DD2于G.
设半圆的半径为r,则πr=![]() ,
,
∴r=20,
∴AG=GB2=20,GD1=30-20=10,
在Rt△GB2D2中,GD2=![]()
∴D1D2=10![]() -10.
-10.
故答案为30![]() ,10
,10![]() -10,
-10,


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,点C在⊙O上,AD垂直于过点C的切线,垂足为D,且∠BAD=80°,则∠DAC的度数是_____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:①垂直于同一直线的两条直线互相平行;②两个无理数的和是无理数;③点![]() 一定不在第四象限;④平方根等于本身的数是
一定不在第四象限;④平方根等于本身的数是![]() 或
或![]() ;⑤若点
;⑤若点![]() 的坐标满足
的坐标满足![]() ,则点
,则点![]() 落在原点上;⑥如果两个角的角平分线互为反向延长线,则这两个角为对顶角.正确个数是( )
落在原点上;⑥如果两个角的角平分线互为反向延长线,则这两个角为对顶角.正确个数是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠C>∠B,AE平分∠BAC,F为射线AE上一点(不与点E重合),且FD⊥BC于D;
(1)如果点F与点A重合,且∠C=50°,∠B=30°,如图1,求∠EFD的度数;
(2)如果点F在线段AE上(不与点A重合),如图2,问∠EFD与∠C﹣∠B有怎样的数量关系?并说明理由.
(3)如果点F在△ABC外部,如图3,此时∠EFD与∠C﹣∠B的数量关系是否会发生变化?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】规定两数a、b之间的一种运算,记作(a,b):如果![]() ,那么(a,b)=c.
,那么(a,b)=c.
例如:因为![]() ,所以(2,8)=3.
,所以(2,8)=3.
(1)根据上述规定,填空:
(5,125)= ,(-2,4)= ,(-2,-8)= ;
(2)小明在研究这种运算时发现一个现象:![]() ,他给出了如下的证明:
,他给出了如下的证明:
设![]() ,则
,则![]() ,即
,即![]()
∴![]() ,即
,即![]() ,
,
∴![]() .
.
请你尝试运用上述这种方法说明下面这个等式成立的理由.
(4,5)+(4,6)=(4,30)
查看答案和解析>>
科目:初中数学 来源: 题型:
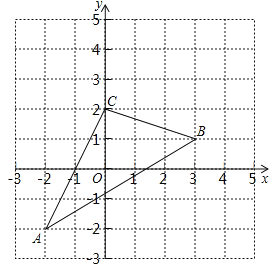
【题目】如图,△ABC在直角坐标系中.
(1)若把△ABC向上平移2个单位,再向左平移1个单位得到△A1B1C1,画出△A1B1C1,并写出点A1,B1,C1的坐标;
(2)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
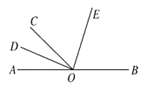
【题目】已知![]() 、
、![]() 、
、![]() 三点在同一条直线上,
三点在同一条直线上,![]() 平分
平分![]() ,
,![]() 平分
平分![]() .
.
(1)若![]() ,求
,求![]() ;
;
(2)若![]() ,求
,求![]() ;
;
(3)![]() 是否随
是否随![]() 的度数的变化而变化?如果不变,度数是多少?请你说明理由,如果变化,请说明如何变化.
的度数的变化而变化?如果不变,度数是多少?请你说明理由,如果变化,请说明如何变化.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,要得到AB∥CD,只需要添加一个条件,这个条件不可以是( )

A. ∠1=∠3 B. ∠B+∠BCD=180°
C. ∠2=∠4 D. ∠D+∠BAD=180°
查看答案和解析>>
科目:初中数学 来源: 题型:
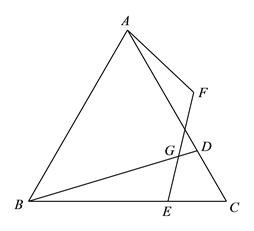
【题目】如图,在等边![]() 中,
中, ![]() 分别是边
分别是边![]() 上的点,且
上的点,且![]() ,
,![]() ,点
,点![]() 与点
与点![]() 关于
关于![]() 对称,连接
对称,连接![]() ,
,![]() 交
交![]() 于
于![]() .
.
(1)连接![]() ,则
,则![]() 之间的数量关系是 ;
之间的数量关系是 ;
(2)若![]() ,求
,求![]() 的大小(用
的大小(用![]() 的式子表示)
的式子表示)
(2)用等式表示线段![]() 和
和![]() 之间的数量关系,并证明.
之间的数量关系,并证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com