
 如图,三角形ABC三个顶点的坐标分别为A(4,3),B(3,1),C(1,2).
如图,三角形ABC三个顶点的坐标分别为A(4,3),B(3,1),C(1,2).分析 (1)先把各点横坐标减去5得出各点坐标,再在坐标系内描出各点,画出△A1B1C1即可;
(2)根据三角形平移的性质画出△A2B2C2,根据各对应点之间的关系即可得出△A1B1C1与△A2B2C2的位置关系.
解答 解:(1)∵A(4,3),B(3,1),C(1,2),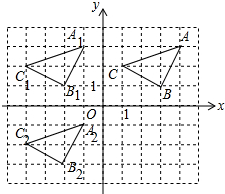
∴由题意A1(-1,3),B1(-2,1),C1(-4,2),
△A1B1C1如图;
(2)将三角形ABC向下平移4个单位,再向左平移5个单位,得到三角形A2B2C2如图所示,
三角形A1B1C1向下平移4个单位即可得到三角形A2B2C2.
点评 本题考查作图变换、坐标与点的位置关系、平移变换等知识,解题的关键是理解左右平移纵坐标不变,横坐标左减右加,上下平移横坐标不变,纵坐标上加下减,属于中考常考题型.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在某段测速公路BC上(公路视为直线)交通管理部门规定汽车的最高行驶速度不能超过60千米/时,并在离该公路100米处设置了一个监测点A,已知点B在A的北偏西60°方向上,点C在点A的偏东40°方向上.(1)监测发现,一辆汽车从点B匀速行驶到点C所用时间为15秒.请你通过计算,判断该越野车在这段限速路上是否超速?(参考数据:sin40°=0.64,tan40°=0.84,$\sqrt{3}$=1.73)
如图,在某段测速公路BC上(公路视为直线)交通管理部门规定汽车的最高行驶速度不能超过60千米/时,并在离该公路100米处设置了一个监测点A,已知点B在A的北偏西60°方向上,点C在点A的偏东40°方向上.(1)监测发现,一辆汽车从点B匀速行驶到点C所用时间为15秒.请你通过计算,判断该越野车在这段限速路上是否超速?(参考数据:sin40°=0.64,tan40°=0.84,$\sqrt{3}$=1.73)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 品种 | 第1年 | 第2年 | 第3年 | 第4年 | 第5 年 |
| 甲 | 9.8 | 9.9 | 10.1 | 10 | 10.2 |
| 乙 | 9.4 | 10.3 | 10.8 | 9.7 | 9.8 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,点A的坐标为(-2,2),点B与点A关于x轴对称,点B先向右平移4个单位长度,再向上平移2个单位长度得到点C.
如图,在平面直角坐标系中,点A的坐标为(-2,2),点B与点A关于x轴对称,点B先向右平移4个单位长度,再向上平移2个单位长度得到点C.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com