
(10分)如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD,等边△ABE.已知∠BAC=30°,EF⊥AB,垂足为F,连接DF.
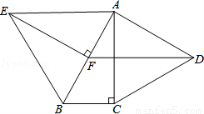
(1)试说明AC=EF;
(2)求证:四边形ADFE是平行四边形.
见解析
【解析】
试题分析:(1)首先Rt△ABC中,由∠BAC=30°可以得到AB=2BC,又因为△ABE是等边三角形,EF⊥AB,由此得到AE=2AF,并且AB=2AF,然后即可证明△AFE≌△BCA,再根据全等三角形的性质即可证明AC=EF;
(2)根据(1)知道EF=AC,而△ACD是等边三角形,所以EF=AC=AD,并且AD⊥AB,而EF⊥AB,由此得到EF∥AD,再根据平行四边形的判定定理即可证明四边形ADFE是平行四边形.
试题解析:(1)∵Rt△ABC中,∠BAC=30°,
∴AB=2BC,
又∵△ABE是等边三角形,EF⊥AB,
∴AB=2AF
∴AF=BC,
在Rt△AFE和Rt△BCA中,
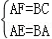 ,
,
∴△AFE≌△BCA(HL),
∴AC=EF;
(2)∵△ACD是等边三角形,
∴∠DAC=60°,AC=AD,
∴∠DAB=∠DAC+∠BAC=90°
∴EF∥AD,
∵AC=EF,AC=AD,
∴EF=AD,
∴四边形ADFE是平行四边形.
考点:1.平行四边形的判定2.全等三角形的判定与性质;


科目:初中数学 来源:2014-2015学年贵州省安顺市九年级第一学期期末教学质量检测数学试卷(解析版) 题型:填空题
在实数范围内定义一种运算“*”,其规则为a*b=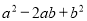 ,根据这个规则求方程(x-4)*1=0的解为 。
,根据这个规则求方程(x-4)*1=0的解为 。
查看答案和解析>>
科目:初中数学 来源:2014-2015学年广东省广州学校九年级上学期期中考试数学试卷(解析版) 题型:解答题
如图,在单位长度为1的正方形网格中,一段圆弧经过网格的交点A、B、C。
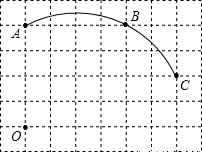
⑴请完成如下操作:①以点O为原点、竖直和水平方向为轴、网格边长为单位长,建立平面直角坐标系;②根据图形提供的信息,作出该圆弧所在圆的圆心D,并连接AD、CD。
⑵请在⑴的基础上,完成下列填空:
①写出点的坐标: C_______、D_______;
②直接写出⊙D半径=_______(结果保留根号);
③直接写出∠ADC=_______;
④若扇形ADC是一个圆锥的侧面展开图,求该圆锥的底面的半径.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年广东省广州学校九年级上学期期中考试数学试卷(解析版) 题型:选择题
如图,⊙O的半径为10cm,现有一根长16cm木棒AB紧贴着⊙O的圆周(即两个端点始终在圆上,按顺时针滑动一周,则木棒AB的中点C在运动的过程中所围成的图形面积为( )
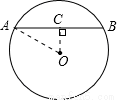
A.16 B.36 C.36π D.无法确定
查看答案和解析>>
科目:初中数学 来源:2014-2015学年广东省广州学校九年级上学期期中考试数学试卷(解析版) 题型:选择题
下列关于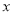 的方程中,一定是一元二次方程的为…( )
的方程中,一定是一元二次方程的为…( )
A. B.
B.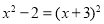 C.
C.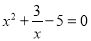 D.
D.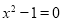
查看答案和解析>>
科目:初中数学 来源:2014-2015学年甘肃省白银市九年级上学期期末考试数学试卷(解析版) 题型:填空题
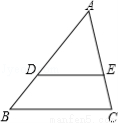
如图,在△ABC中,点D、E分别在AB、AC上,DE∥BC.若AD=4,DB=2,则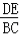 的值为 .
的值为 .
查看答案和解析>>
科目:初中数学 来源:2014-2015学年甘肃敦煌市九年级上学期期中检测数学试卷(解析版) 题型:计算题
计算(每小题5分,共10分)
(1)、用公式法解方程:5x+2=3x2 (2)解方程:3x(x-1)=2-2x
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com