
【题目】如图,在正方形ABCD中,点E是AD边上的一点,AF⊥BE于F,CG⊥BE于G.
(1)若∠FAE=20°,求∠DCG的度数;
(2)猜想:AF,FG,CG三者之间的数量关系,并证明你的猜想.

【答案】(1)70°;(2)CG=AF+FG,理由见解析
【解析】(1)由正方形的性质求得∠ABC=∠D=90°,根据三角形的外角定理求得∠FED,再根据四边形内角和求得结论;
(2)由∠ABF+∠CBG=90°,∠CBG+∠BCG=90°,证得∠ABF=∠BCG,再证得在ABF≌△BCG,AF=BG,由全等三角形的性质证得BF=CG,根据线段的和差和等量代换即可求得结论.
(1)∵四边形ABCD是正方形,
∴ ∠ABC=∠D=90°,
∵AF⊥BE,CG⊥BE,
∴∠AFE=∠CGE=90°,
∵∠FAE=20°,
∴∠FED=∠FAE+∠AFE=20°+90°=110°,
∴∠DCG=360°-∠D-∠FED-∠CGE=360°-90°-110°-90°=70°;
(2)猜想:CG=AF+FG,
证明:∵∠ABF+∠CBG=90°,∠CBG+∠BCG=90°,
∴∠ABF=∠BCG,
在△ABF和△BCG中
∴ABF≌△BCG(AAS),
∴AF=BG,BF=CG,
∴CG=BF=BG+FG=AF+FG.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
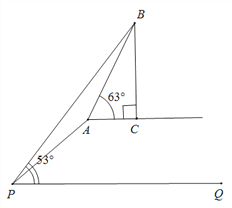
【题目】如图,坡度为1:2的斜坡AP的坡顶有一铁塔BC,在坡底P处测得塔顶B的仰角为53°,在沿斜坡前进![]() 米至A处,测得塔顶B的仰角为63°,已知A、C在同一水平面上.求铁塔BC的高度.
米至A处,测得塔顶B的仰角为63°,已知A、C在同一水平面上.求铁塔BC的高度.
(参考数据:sin63°≈0.89,cos63°≈0.45,tan63°≈2,sin53°≈0.8,cos53°≈0.6,tan53°≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】社区利用一块矩形空地建了一个小型的惠民停车场,其布局如图所示.已知停车场的长为52米,宽为28米,阴影部分设计为停车位,要铺花砖,其余部分是等宽的通道.已知铺花砖的面积为640平方米.
(1)求通道的宽是多少米?
(2)该停车场共有车位64个,据调查分析,当每个车位的月租金为200元时,可全部租出;当每个车位的月租金每上涨10元,就会少租出1个车位.当每个车位的月租金上涨多少元时,停车场的月租金收入为14400元?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,四边形![]() 为正方形,已知点
为正方形,已知点![]() 、
、![]() ,点
,点![]() 、
、![]() 在第二象限内.
在第二象限内.
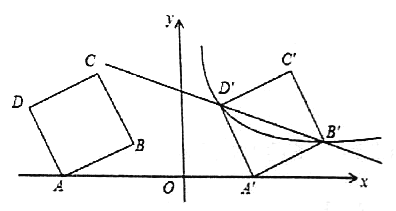
(1)点![]() 的坐标___________;
的坐标___________;
(2)将正方形![]() 以每秒
以每秒![]() 个单位的速度沿
个单位的速度沿![]() 轴向右平移
轴向右平移![]() 秒,若存在某一时刻
秒,若存在某一时刻![]() ,使在第一象限内点
,使在第一象限内点![]() 、
、![]() 两点的对应点
两点的对应点![]() 、
、![]() 正好落在某反比例函数的图象上,请求出此时
正好落在某反比例函数的图象上,请求出此时![]() 的值以及这个反比例函数的解析式;
的值以及这个反比例函数的解析式;
(3)在(2)的情况下,问是否存在![]() 轴上的点
轴上的点![]() 和反比例函数图象上的点
和反比例函数图象上的点![]() ,使得以
,使得以![]() 、
、![]() 、
、![]() 、
、![]() 四个点为顶点的四边形是平行四边形?若存在,请直接写出符合题意的点
四个点为顶点的四边形是平行四边形?若存在,请直接写出符合题意的点![]() 、
、![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义一种对正整数n的“C运算”:①当n为奇数时,结果为3n+1;②当n为偶数时,结果为![]() (其中k是使
(其中k是使![]() 为奇数的正整数),并且运算重复进行.例如,n=66时,其“C运算”如下
为奇数的正整数),并且运算重复进行.例如,n=66时,其“C运算”如下
![]()
若n=26,则第2019次“C运算”的结果是
A. 40 B. 5 C. 4 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在菱形![]() 中,
中,![]() ,点
,点![]() 为
为![]() 边的中点,点
边的中点,点![]() 与点
与点![]() 关于
关于![]() 对称,连接
对称,连接![]() 、
、![]() 、
、![]() ,下列结论:①
,下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ,其中正确的是( )
,其中正确的是( )
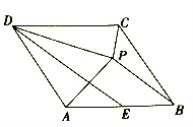
A. ①②B. ①②③C. ①②④D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
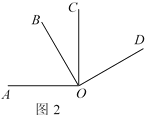
【题目】规律发现:
在数轴上
(1)点M表示的数是2,点N表示的数是8,则线段MN的中点P表示的数为______;
(2)点M表示的数是﹣3,点N表示的数是7,则线段MN的中点P表示的数为_____;发现:点M表示的数是a,点N表示的数是b,则线段MN的中点P表示的数为______.
直接运用:
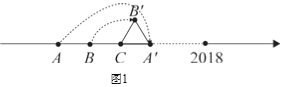
将数轴按如图1所示,从点A开始折出一个等边三角形A'B'C,设点A表示的数为x﹣3,点B表示的数为2x+1,C表示的数为x﹣1,则x值为_____,若将△A'B'C从图中位置向右滚动,则数2018对应的点将与△A'B'C的顶点_______重合.
类比迁移:
如图2:OA⊥OC,OB⊥OD,∠COD=60°,若射线OA绕O点以每秒15°的速度顺时针旋转,射线OB绕O点以每秒10°的速度顺时针旋转,射线OC绕O点以每秒5°的速度逆时针旋转,三线同时旋转,当一条射线与射线OD重合时,三条射线同时停止运动.
①求射线OC和射线OB相遇时,∠AOB的度数;
②运动几秒时,射线OA是∠BOC的平分线?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两地相距300千米,一辆货车和一辆轿车分别从甲地开往乙地(轿车的平均速度大于货车的平均速度),如图,线段![]() 、折线
、折线![]() 分别表示两车离甲地的距离
分别表示两车离甲地的距离![]() (单位:千米)与时间
(单位:千米)与时间![]() (单位:小时)之间的函数关系.
(单位:小时)之间的函数关系.
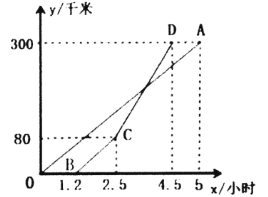
(1)线段![]() 与折线
与折线![]() 中,______(填线段
中,______(填线段![]() 或折线
或折线![]() )表示货车离甲地的距离
)表示货车离甲地的距离![]() 与时间
与时间![]() 之间的函数关系.
之间的函数关系.
(2)求线段![]() 的函数关系式(标出自变量
的函数关系式(标出自变量![]() 取值范围);
取值范围);
(3)货车出发多长时间两车相遇?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com