
分析 (1)根据:潭柘寺游客接待量比2013年增加了25%,且2013年潭柘寺游客接待量为3.2万人次,计算可得;
(2)根据题意分别梳理出潭柘寺、百花山和妙峰山樱桃园在2013-2015年的游客接待量,列表可得;
(3)计算出2014年到2015年门头沟游客接待总量增长百分率,据此估计2016年到2015年门头沟游客接待总量有相近的增长百分率,计算即可.
解答 解:(1)2014年,潭柘寺的游客接待量为3.2×(1+25%)=4(万人次),
故答案为:4;
(2)
(3)∵2014年到2015年门头沟游客接待总量增长百分率为:$\frac{22.1-20}{20}$×100%=10.5%,
∴据此估计2016年到2015年门头沟游客接待总量增长百分率大约为10.5%,
则2016年门头沟游客接待总量为22.1×(1+10.5%)=24.4205(万人次),
故答案为:24.4205,2015年游客接待总量增长百分率为10.5%,估计2016年游客接待总量增长百分率也大约为10.5%.
点评 本题主要考查数据的整理与统计图表的选择与制作,阅读材料理清数据的类型和年份是列表解决问题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
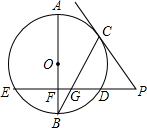 如图,已知AB是⊙O的直径,弦ED⊥AB于点F,点C是劣弧AD上的动点(不与点A、D重合),连接BC交ED于点G.过点C作⊙O的切线与ED的延长线交于点P.
如图,已知AB是⊙O的直径,弦ED⊥AB于点F,点C是劣弧AD上的动点(不与点A、D重合),连接BC交ED于点G.过点C作⊙O的切线与ED的延长线交于点P.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
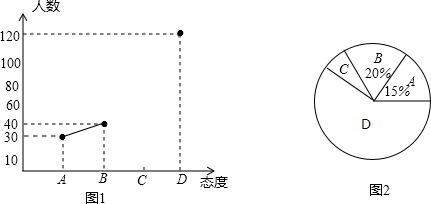
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 四个数2、3、5、4的中位数为4 | |
| B. | 了解重庆初三学生备战中考复习情况,应采用普查 | |
| C. | 小明共投篮25次,进了10个球,则小明进球的概率是0.4 | |
| D. | 从初三体考成绩中抽取100名学生的体考成绩,这100名考生是总体的一个样本 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
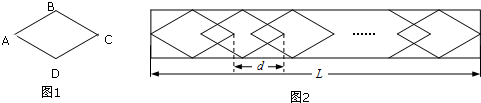
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com