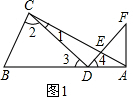
(1)证明:∵∠ACB=90°,
∴∠1+∠2=90°,
∵∠CDF=90°,
∴∠1+∠CED=90°,
∴∠2=∠CED,
∵∠CED=∠FEA,
∴∠FEA=∠2,
∵∠3+∠4=90°,
∠4+∠F=90°,
∠F=∠3,
∴△AEF∽△BCD;
(2)解:过C点作AB边垂线,垂足为M.
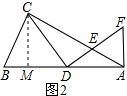
设BM=a,DM=b,则CM=a•tanB=1.5a.
AM=CM•tanB=2.25a,
∵∠DMC+∠FDA=90°,
∠MDC+∠MCD=90°,
∴∠MCD=∠FDA,
∵CD=DF,∠CMD=∠DAF=90°,
∴△CMD≌△DAF,
所以AD=CM=1.5a,
所以AM=AD+MD=1.5a+b=2.25a,
所以b=0.75a,
∴DF=CD=
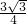
a,
∴AF=

a,BD=a+0.75a,
∴

=
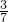
,
则
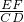
=
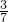
;
(3)解:证出△BCD∽△AEF,
∵CD=DF,AB=13cm,
∴AE=

.
故答案为:

.
分析:(1)由已知条件证明两三角形对应角相等,可以得出△AEF∽△BCD;
(2)过C点作AB边垂线,垂足为M,设BM=a,DM=b,分别求出AD=CM,AM的长,即可得出
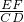
的值;
(3)利用△BCD∽△DAF,即可求出此时AE的长.
点评:此题主要考查了相似三角形的性质与判定,正确的应用两角对应相等的三角形相似是中考中一个热点问题,同学们应熟练掌握此定理.

 ,D为AB边上一点,DE⊥CD于D,交直线AC于E,过点A作AF⊥AB交直线DE于F.
,D为AB边上一点,DE⊥CD于D,交直线AC于E,过点A作AF⊥AB交直线DE于F.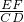 的值;
的值;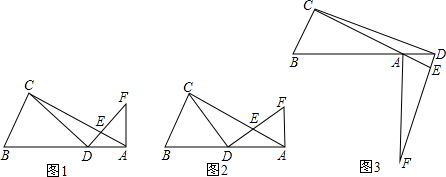
 (1)证明:∵∠ACB=90°,
(1)证明:∵∠ACB=90°,
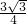 a,
a, a,BD=a+0.75a,
a,BD=a+0.75a, =
=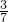 ,
,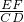 =
=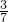 ;
; .
. .
.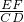 的值;
的值;

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案