Question

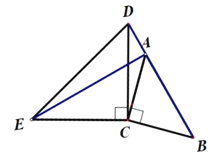
【题目】如图，△ACB和△ECD都是等腰直角三角形，，且点D在BA边的延长线上．

（1）求证：；

（2）求证：；

（3）若，，求△CDE的面积．

Answer 1

【答案】（1）见解析；（2）见解析；（3）．

【解析】

（1）根据△ACB和△ECD都是等腰直角三角形，得到∠BCD=∠ACE，从而可证明

△BCD≌△ACE（SAS）即可；

（2）利用（1）中的△BCD≌△ACE得到对应角相等，结合角度的代换，得到∠DAE=90°，可得，再利用即可得证；

（3）根据△ACB是等腰直角三角形，得到AB=4，计算可得AE=BD=5，利用，得到CE=13，根据直角三角形面积公式计算即得．

（1）∵△ACB和△ECD都是等腰直角三角形，，

∴AC=BC，CD=CE，

∠ACB+∠ACD=∠ECD+∠ACD，

∴∠BCD=∠ACE，

∴△BCD≌△ACE（SAS），

∴AE=BD；

（2）∵△BCD≌△ACE，

∴∠BDC=∠AEC，

∵∠DCE=90°，

∴∠CDE+∠DEC=90°，

∴∠CDE+∠DEA+∠AEC=90°，

∴∠CDE+∠DEA+∠BDC=90°，

∴∠BDE+∠AED=90°，

∴∠DAE=90°，

∴，

∵△DCE是等腰直角三角形，∠DCE=90°，

∴，

∴；

（3）∵∠ACB=90°，BC=AC=2，

∴AB=，

∴BD=1+4=5，

∴AE=BD=5，

∵，

∴，

∴=13，

∴，

故答案为：．