
【题目】如图1,函数y=﹣x+4的图象与坐标轴交于A、B两点,点M(2,m)是直线AB上一点,点N与点M关于y轴对称.

(1)填空:m= ;
(2)点P在平面上,若以A、M、N、P为顶点的四边形是平行四边形,直接写出点P的坐标;
(3)如图2,反比例函数![]() 的图象经过N、E(x1,y1)、F(x2,y2)三点.且x1>x2,点E、F关于原点对称,若点E到直线MN的距离是点F到直线MN的距离的3倍,求E、F两点的坐标.
的图象经过N、E(x1,y1)、F(x2,y2)三点.且x1>x2,点E、F关于原点对称,若点E到直线MN的距离是点F到直线MN的距离的3倍,求E、F两点的坐标.
【答案】(1)2.
(2)点P的坐标为(0,0)、(8,0)或(﹣4,4).
(3)点E(4,﹣1),点F(﹣4,1).
【解析】
试题分析:(1)由点M的横坐标利用一次函数图象上点的坐标特征可得出关于m的一元一次方程,解方程即可得出结论;
(2)连接AN,分别以△AMN的三条边为对角线找平行四边形,由直线AB的解析式可找出点A的坐标,再由M、N关于y轴对称即可得出点N的坐标,根据平行四边形对角线互相平分的性质,结合点A、M、N的坐标即可得出点P的坐标;
(3)根据点N的坐标利用反比例函数图象上点的坐标特征即可求出反比例函数的解析式,由点E、F关于原点对称,可得出x1=﹣x2,y1=﹣y2,再根据M、N的坐标求出直线MN的关系式,分点F在直线MN的上方或下方两种情况,结合点E到直线MN的距离是点F到直线MN的距离的3倍,即可得出y1、y2的关系,由此即可得出点E、F的坐标.
解:(1)∵点M(2,m)是直线AB:y=﹣x+4上一点,
∴m=﹣2+4,解得:m=2.
故答案为:2.
(2)连接AN,以A、M、N、P为顶点的平行四边形分三种情况,如图1所示.

∵直线y=﹣x+4的图象与坐标轴交于A、B两点,
∴A(4,0),B(0,4),
∵点N与点M关于y轴对称,点M(2,2),
∴N(﹣2,2).
以A、M、N、P为顶点的平行四边形分三种情况:
①当线段AN为对角线时,
∵A(4,0)、M(2,2)、N(﹣2,2),
∴点P的坐标为(4﹣2﹣2,0+2﹣2),即(0,0);
②当线段AM为对角线时,
∵A(4,0)、M(2,2)、N(﹣2,2),
∴点P的坐标为(4+2﹣(﹣2),0+2﹣2),即(8,0);
③当线段MN为对角线时,
∵A(4,0)、M(2,2)、N(﹣2,2),
∴点P的坐标为(2﹣2﹣4,2+2﹣0),即(﹣4,4).
综上可知:若以A、M、N、P为顶点的四边形是平行四边形,点P的坐标为(0,0)、(8,0)或(﹣4,4).
(3)∵反比例函数![]() 的图象经过N(﹣2,2)、E(x1,y1)、F(x2,y2)三点,
的图象经过N(﹣2,2)、E(x1,y1)、F(x2,y2)三点,
∴k=﹣2×2=﹣4,
∴反比例函数解析式为![]() .
.
∵点E、F关于原点对称,
∴x1=﹣x2,y1=﹣y2,
∵x1>x2,
∴点E在第四象限,点F在第二象限.
直线MN的关系式为y=2,
点E到直线MN的距离是点F到直线MN的距离的3倍.
①当点F在直线MN的上方时,
点E到直线MN的距离是:2﹣y1,点F到直线MN的距离是:y2﹣2,
∴3(y2﹣2)=2﹣y1,y1=﹣y2,
∴y1=﹣4,y2=4,
∴点E(1,﹣4),点F(﹣1,4);
②当点F在直线MN的下方时,
点E到直线MN的距离是:2﹣y1,点F到直线MN的距离是:2﹣y2,
∴3(2﹣y2)=2﹣y1,y1=﹣y2,
∴y1=﹣1,y2=1,
∴点E(4,﹣1),点F(﹣4,1).


科目:初中数学 来源: 题型:
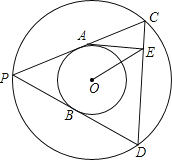
【题目】如图,以O为圆心的两个同心圆,大圆半径为5,小圆半径为![]() ,点P为大圆上的一点,PC、PB切小圆于点A、点B,交大圆于C、D两点,点E为弦CD上任一点,则AE+OE的最小值为 .
,点P为大圆上的一点,PC、PB切小圆于点A、点B,交大圆于C、D两点,点E为弦CD上任一点,则AE+OE的最小值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果第一次租用2辆A型车和1辆B型车装运水果,一次运货10吨;第二次租用1辆A型车和2辆B型车装水果,一次运货11吨(两次运货都是满载)
①求每辆A型车和B型车满载时各装水果多少吨?
②现有31吨水果需运出,计划同时租用A型车和B型车一次运完,且每辆车都恰好装满,请设计出有哪几种租车方案?
③若A型车每辆租金200元,B型车每辆租金300元,问哪种租车方案最省钱,最省钱的方案总共租金多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义一种新运算“⊕”:a⊕b=a﹣2b,比如:2⊕(﹣3)=2﹣2×(﹣3)=2+6=8.
(1)求(﹣3)⊕2的值;
(2)若(x﹣3)⊕(x+1)=1,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列式子去括号正确的是( )
A. -(2a+3b-5c)=-2a-3b+5c B. 5a+2(3b-3)=5a+6b-3
C. 3a-(b-5)=3a-b-5 D. -3(3x-y+1)=-9x+3y-1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com