

���� ��1����ͼ1����DC��ȡһ��F��ʹDF=OB������AF��֤����DAC�ա�BAE��DC=BE����FC=OE����֤����ADF�ա�ABO�͡�AFC�ա�AOE���á�AFOΪ�ȱ������Σ���AO=OF���Ӷ��ó����ۣ�
��2���������߹�������ֱ�������κ�ȫ�������Σ����ݣ�1����֤��CM=BN��CM��BN�������������ε���λ�߿ɵ�DF��MC��DF=MC��EF��BN��EF=BN�����֤���ı���PFQO�Ǿ��Σ��ó����ۣ�
��3�����������������Σ�������ͼ1���Ƶ�ȫ�������Σ�֤����ABJ�ա�AIC����BJ=CI��֤����ICN�ա�JBM����IN=JM����$\frac{BD}{BI}=\frac{BF}{BN}=\frac{DF}{IN}$=$\frac{1}{3}$����$\frac{EF}{JM}=\frac{1}{3}$��DF=EF���Ӷ��ó���DEF�ǵȱ������Σ�
��4������DEFΪ����ֱ�������Σ������ǣ��������߹������������Σ��루3��ͬ�����ã�$\frac{EF}{OM}$=$\frac{DF}{PN}$��EF=DF����ͬ���þ���FGHQ����ó����ۣ�
���  ֤������1����ͼ1����DC��ȡһ��F��ʹDF=OB������AF��
֤������1����ͼ1����DC��ȡһ��F��ʹDF=OB������AF��
�ߡ�ABD����ACE���ǵȱ������Σ�
��AD=AB��AC=AE����DAB=��CAE=60�㣬
���DAB+��BAC=��CAE+��BAC��
����DAC=��BAE��
���DAC�ա�BAE��
���CDA=��ABE��CD=BE��
���ADF�ա�ABO��
��AF=AO��
��CD=BE��DF=OB��
��CF=OE��
���AFC�ա�AOE��
���FAC=��OAE��
���FAO+��OAC=��EAC+��OAC��
���FAO=��EAC=60�㣬
���AFOΪ�ȱ������Σ�
��AO=OF��
��FC=OE��
��FO+OC=OE��
��OA+OC=OE��
��2����ͼ2��DF=EF��DF��EF�������ǣ�
�ӳ�BD��M��ʹBD=DM���ӳ�CE��N��ʹCE=EN������CM��AM��AN��BN��
�ߡ�ADB����ACE�ǵ���ֱ�������Σ�
��AD=BD=DM��AE=EC=EN��
���ADM����AENҲ�ǵ���ֱ�������Σ���AM=AB��AC=AN��
���MAB=��MAD+��BAD=45��+45��=90�㣬
ͬ����CAN=90�㣬
���MAB+��BAC=��CAN+��BAC��
����MAC=��BAN��
���MAC�ա�BAN��
��MC=BN����CMA=��ABN��
�ڡ�AMG�У���AMG+��AGM=90�㣬
�ߡ�AGM=��CGB��
���ABN+��CGB=90�㣬
���GOB=90�㣬
��MC��BN��
��D��BM���е㣬F��BC���е㣬
��DF��MC��DF=MC��
ͬ���ã�EF��BN��EF=BN��
��DF=EF���ı���PFQO��ƽ���ı��Σ�
�ߡ�POQ=90�㣬
��?PFQO�Ǿ��Σ�
���DFE=90�㣬
��DF��EF��
��3����ͼ3����DEF�ǵȱ������Σ������ǣ�
��A��AD�Ĵ��߽�BD�ӳ�����I����A��AE�Ĵ��߽�CE�ӳ�����J��
��B��BF�Ĵ��߽�CF�ӳ�����M����C��CF�Ĵ��߽�BF�ӳ�����N��
����CI��BJ��IN��JM��
�á�ABI����ACJ����BCN����MBCΪ����Ϊ120��ĵ��������Σ�
��BD=AD=x����ID=2x��
��$\frac{BD}{BI}$=$\frac{1}{3}$��
ͬ��$\frac{BF}{BN}=\frac{CF}{CM}=\frac{CE}{CJ}=\frac{1}{3}$��
�ߡ�IBN=��DBF��
���DBF�ס�IBN��
��$\frac{DF}{IN}$=$\frac{BF}{BN}$=$\frac{1}{3}$��
ͬ��$\frac{EF}{JM}$=$\frac{1}{3}$��
��$\frac{DF}{IN}=\frac{EF}{JM}$��
�ߡ�CAJ=��BAI=90��+30��=120�㣬
���CAI=��BAJ��
��AB=AI��AC=AJ��
���ABJ�ա�AIC��
��BJ=CI��
�ߡ�BCN����MBC�ǵ��������Σ�
��BC=CN��BC=BM��
��BM=CN��
�ߡ�JBA=��AIC��
�����������ڽǺͶ����ã���JBC+��ICB=120�㣬
�ߡ�MBC=��BCN=120�㣬
���JBC+��ICB+��MBC+��BCN=360�㣬
���JBM+��ICB+��BCN=360�㣬
�ߡ�ICN+��ICB+��BCN=360�㣬
���JBM=��ICN��
���ICN�ա�JBM��
��IN=JM��
��DF=EF��
ͬ��DE=DF��
��DF=EF=DE��
���DEF�ǵȱ������Σ�
��4����DEFΪ����ֱ�������Σ������ǣ�
��ͼ4���ֱ��A��B��C��������ABP����ACO����BMF����FCN��
����PC��BO��
��AB=AP����ABD=45�㣬
ͬ����CAO=90�㣬
���PAC=90��+��BAC����BA0=90��+��BAC��
���PAC=��BAO��
��AO=AO��
���BAO�ա�PAC��
��BO=PC��
��ͼ5������PN��OM���ɣ�3��ͬ���ã�PC��BO��
��BF=BM��FC=CN��
��BM=CN��
�ߡ�BMC=30�㣬��BCM=15�㣬
���MBC=135�㣬
ͬ����BCN=135�㣬
���OBC+��MBC+��BCN+��PCB=360�㣬
���OBM+��BCN+��PCB=360�㣬
�ߡ�PCN+��BCN+��PCB=360�㣬
���OBM=��PCN��
���OBM�ա�PCN��
��OM=PN��
��ͼ6����E��EQ��AC��Q��
��EQ=x����CQ=x��AE=2x��
�ɹ��ɶ����ã�AQ=$\sqrt{3}$x��CE=$\sqrt{2}$x��
��AC=AO=��1+$\sqrt{3}$��x��
�ߡ�AOC�ǵ���ֱ�������Σ�
��OC=$\sqrt{2}$AC=$\sqrt{2}$��1+$\sqrt{3}$��x��
��$\frac{CE}{CO}$=$\frac{\sqrt{2}x}{\sqrt{2}��1+\sqrt{3}��x}$=$\frac{1}{1+\sqrt{3}}$��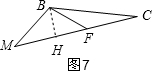
��ͼ7����B��BH��MC��H��
�ߡ�HFB=30�㣬
��BH=x����FH=$\sqrt{3}$x��BF=FC=2x��
��MH=HF=$\sqrt{3}$x��
��$\frac{CF}{CM}$=$\frac{2x}{2x+2\sqrt{3}x}$=$\frac{1}{1+\sqrt{3}}$��
��$\frac{CE}{CO}=\frac{CF}{CM}$��
�ɣ�3��ͬ���ã�$\frac{EF}{OM}$=$\frac{DF}{PN}$��
��EF=DF��
ͬ���ã��ı���FGHQΪƽ���ı��Σ�
�ߡ�QHG=90�㣬
��?FGHQ����
���DFE=90�㣬
���DEFΪ����ֱ�������Σ�
���� �����������ε��ۺ��⣬ͼ�νϸ��ӣ��ۺ��Խ�ǿ�������������������������εĸ���������������ȫ�������Σ����������������ε��ж������ʵó�����ȵĽ��ۣ��Ӷ����Եó�����������Σ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| ����x��kg�� | �ۼ�y��Ԫ�� |
| 1 | 8+0.4 |
| 2 | 16+0.4 |
| 3 | 24+0.4 |
| �� |
| A�� | y=8x | B�� | y=8x+0.4 | C�� | y=8.4x | D�� | y=8+0.4x |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 13 | B�� | 14 | C�� | 15 | D�� | 16 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ������ABCD�У�AB=4��AD=3����DAB�Ľ�ƽ���߽���CD�ڵ�E����P������AE����ÿ��$\sqrt{2}$����λ���ȵ��ٶ�������AE����ӵ�A��ʼ�˶�������P��PQ��AB�ڵ�Q����PQΪ��������ƽ���ı���PQMN����N������AE�ϣ���AP=PN����P���˶�ʱ��Ϊt�룮
��ͼ������ABCD�У�AB=4��AD=3����DAB�Ľ�ƽ���߽���CD�ڵ�E����P������AE����ÿ��$\sqrt{2}$����λ���ȵ��ٶ�������AE����ӵ�A��ʼ�˶�������P��PQ��AB�ڵ�Q����PQΪ��������ƽ���ı���PQMN����N������AE�ϣ���AP=PN����P���˶�ʱ��Ϊt�룮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ����BAC=90�㣬AD��BC������ΪD��������Ľ�������ȷ�ĸ���Ϊ��������
��ͼ����BAC=90�㣬AD��BC������ΪD��������Ľ�������ȷ�ĸ���Ϊ��������| A�� | 2 | B�� | 3 | C�� | 4 | D�� | 5 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com