
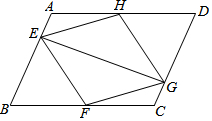
 如图,在?ABCD中,点E、F、G、H分别在边AB、BC、CD、DA上,AE=CG,AH=CF,且EG平分∠HEF.
如图,在?ABCD中,点E、F、G、H分别在边AB、BC、CD、DA上,AE=CG,AH=CF,且EG平分∠HEF.分析 (1)根据全等三角形的判定定理SAS证得结论;
(2)欲证明四边形EFGH是菱形,只需推知四边形EFGH是平行四边形,然后证得该平行四边形的邻边相等即可.
解答 证明:(1)∵四边形ABCD是平行四边形,
∴∠A=∠C.
∴在△AEH与△CGF中,$\left\{\begin{array}{l}{AE=CG}\\{∠A=∠C}\\{AH=CF}\end{array}\right.$,
∴△AEH≌△CGF(SAS);
(2)∵四边形ABCD是平行四边形,
∴AD=BC,AB=CD,∠B=∠D.
∵AE=CG,AH=CF,
∴EB=DG,HD=BF.
∴△BEF≌△DGH.
∴EF=HG.
又∵△AEH≌△CGF,
∴EH=GF.
∴四边形HEFG为平行四边形.
∴EH∥FG,
∴∠HEG=∠FGE.
∵EG平分∠HEF,
∴∠HEG=∠FEG,
∴∠FGE=∠FEG,
∴EF=GF,
∴四边形EFGH是菱形.
点评 本题考查了菱形的判定,全等三角形的判定与性质以及平行四边形的判定与性质.注意:本题菱形HEFG的判定是在平行四边形HEFG的基础上推知的.


 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
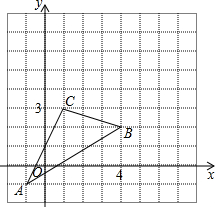 如图,△ABC在直角坐标系中,
如图,△ABC在直角坐标系中,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
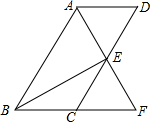 如图,四边形ABCD为平行四边形,∠BAD的角平分线AF交CD于点E,交BC的延长线于点F.
如图,四边形ABCD为平行四边形,∠BAD的角平分线AF交CD于点E,交BC的延长线于点F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com