
【题目】已知:在△ABC中,∠ABC=3∠C,∠BAC的平分线AD交BC于D,BE⊥AD于E.
(1)如图l,求证:AC﹣AB=2BE.
(2)如图2,将∠DCA沿直线AC翻折,交BA的延长线于点M,连接MD交AC于点N;MA=BA,BE=1,AB=![]() ,求AN的长.
,求AN的长.

【答案】(1)见解析;(2)2-![]() .
.
【解析】
(1)延长BE交AC于F.由AD平分∠BAC得∠1=∠2,再由BE⊥AD及公共边AE可证△AEB≌△AEF,由全等的性质可知AB=AF,∠3=∠4,BE=FE,则BF=2BE;由三角形外角和可知∠4=∠5+∠C,则∠ABC=∠3+∠5=∠4+∠5=2∠5+∠C,再由∠ABC=3∠C可知∠5=∠C,则CF=BF=2BE,据此即可证明;
(2)作AH⊥BC于H,AK⊥CM于K,易证△AHB≌△AKM,据此可证明△BCA≌△MCA,可得∠CAB=∠CAM=![]() ;再由勾股定理计算可得AE=BE=1,由题干条件及上问证明可得AB=AD,从而得到MD⊥BC,进而得到∠NCD=∠BMD;再通过△AEB是直角等腰三角形可证明△MDC也是直角等腰三角形,可证明△MBD≌△CND,则可通过计算AC和CN的长度,通过AN=AC﹣CN进行计算.
;再由勾股定理计算可得AE=BE=1,由题干条件及上问证明可得AB=AD,从而得到MD⊥BC,进而得到∠NCD=∠BMD;再通过△AEB是直角等腰三角形可证明△MDC也是直角等腰三角形,可证明△MBD≌△CND,则可通过计算AC和CN的长度,通过AN=AC﹣CN进行计算.
解:(1)延长BE交AC于F.
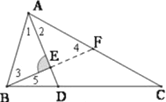
∵AD平分∠BAC,
∴∠1=∠2.
∵BE⊥AD,
∴∠AEB=AEF=90°.
∵∠1=∠2,∠AEB=AEF=90°,AE=AE,
∴△AEB≌△AEF(ASA)
∴AB=AF,∠3=∠4,BE=FE,
∴BF=2BE.
∵∠4=∠5+∠C,
∴∠3=∠5+∠C,
∵∠ABC=∠3+∠5,
∴∠ABC=∠5+∠C+∠5=2∠5+∠C=3∠C,
∴∠5=∠C,
∴CF=BF=2BE.
∵AC﹣AF=FC,
∴AC﹣AB=2BE;
(2)作AH⊥BC于H,AK⊥CM于K,
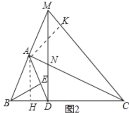
∵∠ACH=∠ACK,
∴AH=AK,
∵AB=AM,
∴△AHB≌△AKM,
∴∠ABH=∠AMK,
∴CB=CM,
∵AC=AC,CB=CM,AB=AM,
∴△BCA≌△MCA,
∴∠CAB=∠CAM=![]() ,
,
∵BE⊥AD,
∴∠AEB=90°.
∵BE=1,AB=![]() ,由勾股定理,得
,由勾股定理,得
∴AE=1,
∴AE=BE,
∴∠BAE=∠ABE
由上问证明可知,∠BAN=∠CAD,∠EBD=∠ACB,
∴∠ABD=∠ABE+∠EBD,∠ADB=∠CAD+∠ACB,
∴∠ABD=∠ADB,
∴AB=AD,
∵AM=AB,
∴AD=AB=AM,
∴△DBM是直角三角形,
∵∠MBD+∠NCD=90°,∠MBD+∠BMD=90°,
∴∠NCD=∠BMD,
∵BE⊥AD,AE=BE,
∴∠BAE=∠ABE=45°.
∵AD平分∠BAC,
∴∠BAC=2∠BAD=90°,
∴∠ABC+∠ACB=90°.
∵∠ABC=3∠ACB,
∴∠ACB=22.5°,
∴∠BCM=45°,
∴∠DMC=45°,
∴∠BCM=∠DMC,
∴DM=DC.
∵∠BDM=∠CDM=90°,DM=DC,∠BMD=∠NCD,
∴△MBD≌△CND(ASA),
∴CN=BM=2AB=2![]() ,
,
∴AC=2BE+AB=2+![]() ,
,
∴AN=AC﹣CN=2﹣![]() .
.


科目:初中数学 来源: 题型:
【题目】为了更好地治理水质,保护环境,某污水处理公司决定购买10台污水处理设备,现有A、B两种设备可供选择,月处理污水分别为240m3/月、200m3/月.经调查:购买一台A型设备比购买一台B型设备多2万元,购买2台A型设备比购买3台B型设备少8万元.
(1)A、B两种型号的设备每台的价格是多少?
(2)若污水处理公司购买设备的预算资金不超过125万元,你认为该公司有哪几种购买方案?
(3)若每月需处理的污水约2040m3,在不突破(2)中资金预算的前提下,为了节约资金,又要保证治污效果,请你为污水处理公司设计一种最省钱的方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是交警在一个路口统计的某个时段来往车辆的车速(单位:千米/时)情况.

(1)这些车的平均速度为__________千米/时;
(2)车速的众数是__________;
(3)车速的中位数是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,点![]() 是
是![]() 的边
的边![]() 上一点,连结
上一点,连结![]() 把
把![]() 沿
沿![]() 折叠,使点
折叠,使点![]() 落在
落在![]() 处,令
处,令![]() .
.



(1)如图②,当点![]() 落在四边形
落在四边形![]() 内部时,若
内部时,若![]() ,则
,则![]() 的度数为 ;
的度数为 ;
(2)事实上,当点![]() 落在四边形
落在四边形![]() 内部时,
内部时,![]() 与
与![]() 之间的数量关系始终保持不变,请写出
之间的数量关系始终保持不变,请写出![]() 与
与![]() 之间的数量关系,并利用图②进行证明;
之间的数量关系,并利用图②进行证明;
(3)如图③,当点![]() 落在四边形
落在四边形![]() 外部时,直接写出
外部时,直接写出![]() 与
与![]() 之间的数量关系为 .
之间的数量关系为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c与x轴交于A(1,0),B(﹣3,0)
(1)求这条抛物线的解析式;
(2)设(1)中的抛物线交y轴于C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出点Q的坐标;若不存在说明理由;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点 A(0,4)在 y 轴上,点 B(b,0)是 x 轴上一动点,且 4< b <4,△ABC 是以 AB 为直角边,B 为直角顶点的等腰直角三角形.
(1)求点 C 的坐标(用含 b 的式子表示);
(2)以 x 轴为对称轴,作点 C 的对称点 C 连接 BC、AC,请把图形补充完整,并求出△ABC的面积(用含 b 的式子表示);
(3)点 B 在运动过程中, OAC 的度数是否发生变化,若变化请说明理由;若不变化,请直接 写出 OAC 的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知经过原点的抛物线y=ax2+bx+c(a≠0)的对称轴是直线x=﹣1,下列结论中: ①ab>0,②a+b+c>0,③当﹣2<x<0时,y<0.
正确的个数是( )
A.0个
B.1个
C.2个
D.3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学改革学生的学习模式,变“老师要学生学习”为“学生自主学习”,培养了学生自主学习的能力.小华与小明同学就“你最喜欢哪种学习方式”随机调查了他们周围的一些同学,根据收集到的数据绘制了以下两个不完整的统计图(如图).


请根据上面两个不完整的统计图回答以下4个问题:
(1)这次抽样调查中,共调查了_____名学生.
(2)补全条形统计图中的缺项.
(3)在扇形统计图中,选择教师传授的占_____%,选择小组合作学习的占_____%.
(4)根据调查结果,估算该校1800名学生中大约有_____人选择小组合作学习模式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() ,
,![]() ,
,![]() ,
,![]() 分别平分
分别平分![]() 的外角
的外角![]() ,内角
,内角![]() ,外角
,外角![]() .以下结论:①
.以下结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() 平分
平分![]() ;⑤
;⑤![]() .其中正确的结论有______________.(把正确结论序号填写在横线上)
.其中正确的结论有______________.(把正确结论序号填写在横线上)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com