
如图1,将两个完全相同的三角形纸片ABC和DEC重合放置,其中∠C=90º,∠B=∠E=30º.
(1)操作发现
如图2,固定△ABC,使△DEC绕点C顺时针旋转.当点D恰好落在AB边上时,填空:

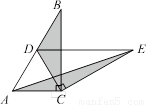
线段DE与AC的位置关系是 ;
设△BDC的面积为S1,△AEC的面积为S2,则S1与S2的数量关系是 ,证明你的结论;
猜想论证
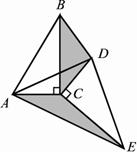
当△DEC绕点C旋转到图3所示的位置时,小明猜想(1)中S1与S2的数量关系仍然成立,并尝试分别作出了△BDC和△AE中BC,CE边上的高,请你证明小明的猜想.
(1)①平行,②相等;(2)见解析.
【解析】
试题分析:(1)①根据旋转的性质可得AC=CD,然后求出△ACD是等边三角形,根据等边三角形的性质可得∠ACD=60º,然后根据内错角相等,两直线平行解答;
②根据等边三角形的性质可得AC=AD,再根据直角三角形30º角所对的直角边等于斜边的一半求出AC=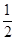 AB,然后求出AC=BE,再根据等边三角形的性质求出点C到AB的距离等于点D到AC的距离,然后根据等底等高的三角形的面积相等解答;
AB,然后求出AC=BE,再根据等边三角形的性质求出点C到AB的距离等于点D到AC的距离,然后根据等底等高的三角形的面积相等解答;
(2)根据旋转的性质可得BC=CE,AC=CD,再求出∠ACN=∠DCM,然后利用"角角边"证明△ACN和△DCM全等,根据全等三角形对应边相等可得AN=DM,然后利用等底等高的三角形的面积相等证明;
试题解析:
(1)①线段DE与AC的位置关系是 平行 .②S1与S2的数量关系是 相等 .
证明:如图2,过D作DN⊥AC交AC于点N,过E作EM⊥AC交AC延长线于M,过C作CF⊥AB交AB于点F.
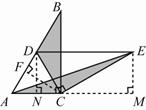
由①可知△ADC是等边三角形,DE∥AC,
∴DN=CF,DN=EM.
∴CF=EM.
∵∠ACB=90º,∠B=30º,
∴AB=2AC.
又∵AD=AC,
∴BD=AC.
∵S1=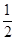 CF·BD,S2=
CF·BD,S2=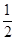 AC·EM,
AC·EM,
∴S1=S2.
证明:如图3,作DG⊥BC于点G,AH⊥CE交EC延长线于点H.
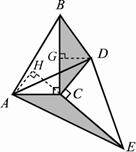
∵∠DCE=∠ACB=90º∴∠DCG+∠ACE=180º.
又∵∠ACH+∠ACE=180º,∴∠ACH=∠DCG.
又∵∠CHA=∠CGD=90º,AC=CD,
∴△AHC≌△DGC.
∴AH=DG.
又∵CE=CB,
∴S1=S2.
考点:全等三角形的判定与性质.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
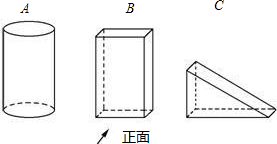 如图所给的A、B、C三个几何体中,按箭头所示的方向为它们的正面,设A、B、C三个几何体的主视图分别是A1、B1、C1;左视图分别是A2、B2、C2,俯视图分别是A3、B3、C3.
如图所给的A、B、C三个几何体中,按箭头所示的方向为它们的正面,设A、B、C三个几何体的主视图分别是A1、B1、C1;左视图分别是A2、B2、C2,俯视图分别是A3、B3、C3.
查看答案和解析>>
科目:初中数学 来源:2012届江苏省宜兴外国语学校九年级下期二模考试数学试卷(带解析) 题型:解答题
如图所给的A、B、C三个几何体中,按箭头所示的方向为它们的正面,设A、B、C三个几何体的主视图分别是A1、B1、C1;左视图分别是A2、B2、C2;俯视图分别是A3、B3、C3.
(1)请你分别写出A1、A2、A3、B1、B2、B3、C1、C2、C3图形的名称;
(2)小刚先将这9个视图分别画在大小、形状完全相同的9张卡片上,并将画有A1、A2、A3的三张卡片放在甲口袋中,画有B1、B2、B3的三张卡片放在乙口袋中,画有C1、C2、C3的三张卡片放在丙口袋中,然后由小亮随机从这三个口袋中分别抽取一张卡片.
① 通过画树状图,求出小亮随机抽取的三张卡片上的图形名称都相同的概率;
② 小亮和小刚做游戏,游戏规则规定:在小亮随机抽取的三张卡片中只有两张卡片上的图形名称相同时,小刚获胜;三张卡片上的图形名称完全不同时,小亮获胜.这个游戏对双方公平吗?为什么?
查看答案和解析>>
科目:初中数学 来源:2011-2012学年江苏省九年级下期二模考试数学试卷(解析版) 题型:解答题
如图所给的A、B、C三个几何体中,按箭头所示的方向为它们的正面,设A、B、C三个几何体的主视图分别是A1、B1、C1;左视图分别是A2、B2、C2;俯视图分别是A3、B3、C3.
(1)请你分别写出A1、A2、A3、B1、B2、B3、C1、C2、C3图形的名称;
(2)小刚先将这9个视图分别画在大小、形状完全相同的9张卡片上,并将画有A1、A2、A3的三张卡片放在甲口袋中,画有B1、B2、B3的三张卡片放在乙口袋中,画有C1、C2、C3的三张卡片放在丙口袋中,然后由小亮随机从这三个口袋中分别抽取一张卡片.
① 通过画树状图,求出小亮随机抽取的三张卡片上的图形名称都相同的概率;
② 小亮和小刚做游戏,游戏规则规定:在小亮随机抽取的三张卡片中只有两张卡片上的图形名称相同时,小刚获胜;三张卡片上的图形名称完全不同时,小亮获胜.这个游戏对双方公平吗?为什么?

查看答案和解析>>
科目:初中数学 来源:第9章《概率的简单应用》常考题集(01):9.1 抽签方法合理吗(解析版) 题型:解答题


查看答案和解析>>
科目:初中数学 来源:2008-2009学年九年级数学第三次月考测试卷(解析版) 题型:解答题


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com