
����Ŀ��ʮһ�ڼ䣬С��һ��һ��ȥ���Σ���ͼ��С����Ƶ�ij���ξ����ͼֽ������������ͬ��С��������ɵģ���С�����εı߳�����ʵ�ʳ���100m���ڸ�ͼֽ�Ͽɿ���������־�Ծ���A��B���������ʵ���ƽ��ֱ������ϵ�����A����3��1����B����3����3��������������C��1��3����λ��������
��1������ͼ�л���ƽ��ֱ������ϵ�����������C��λ�ã�
��2��ƽ��ֱ������ϵ������ԭ��Ϊ��O����ACO��ֱ�������������жϲ�˵�����ɣ�
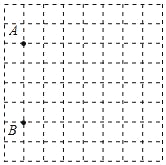
���𰸡���1������������2����ACO��ֱ�������Σ�
��������
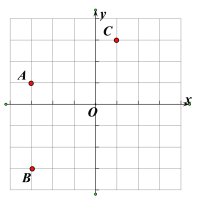
(1)����A����������ƽ��3����λ�õ��ĵ���y�ᣬ����ƽ��1����λ�õ��ĵ���x�ᣬ�ɵ�ƽ��ֱ������ϵ������C�����꣬�ɵô𰸣�
(2)���ݹ��ɶ��������ACO�������ߣ�Ȼ�����ù��ɶ������涨���ж���ֱ��������.
��1����ͼ:
��2����ACO��ֱ�������Σ�
�������£�
��A����3��1����C��1��3����
��OA=![]() =
=![]() ��OC=
��OC=![]() =
=![]() ��AC=
��AC=![]() =2
=2![]() ��
��
��OA2+OC2=AC2��
���AOC��ֱ�������Σ���AOC=90�㣮
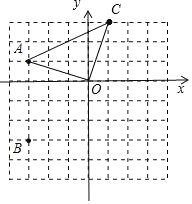
�ʴ�Ϊ����1������������2����ACO��ֱ��������.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ����ƽ��ֱ������ϵ�У�OΪ����ԭ�㣬�ı���OABC�����Σ���A��C������ֱ�Ϊ![]() ��
��![]() ����D��OA���е㣬��P��BC�����˶�����
����D��OA���е㣬��P��BC�����˶�����![]() �ǵ���������ʱ������������Ϊ_______________��
�ǵ���������ʱ������������Ϊ_______________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���ABCD�У���BAD=��CDA=90����AB=1��CD=2����A��B��D����ġ�O�ֱ�BC��CD�ڵ�E��M����CE=1�����н��ۣ���DM=CM����![]() ���ۡ�O��ֱ��Ϊ2����AE=AD��������ȷ�Ľ�����_____������ţ���
���ۡ�O��ֱ��Ϊ2����AE=AD��������ȷ�Ľ�����_____������ţ���
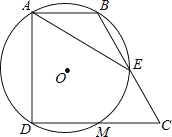
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�AB=AC����D��E��BC�ϣ�����AD��AE�����ֻ����һ������ʹ��DAB=��EAC�������ӵ���������Ϊ�� ��

A. BD=CE B. AD=AE C. DA=DE D. BE=CD
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�߶�AB=6��CΪ�߶�AB�ϵ�һ�����㣨����A��B�غϣ������߶�AC�Ƶ�A��ʱ����ת120��õ�AD�����߶�BC�Ƶ�B˳ʱ����ת120��õ�BE����O�������CDE������O�İ뾶��СֵΪ_____��
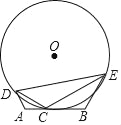
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У���֪![]() ��
��![]() ����
����![]() ��
��![]() ��
��![]() ���Ϸ������ı���
���Ϸ������ı���![]() �����Ϊ32��
�����Ϊ32��
��1�����ı���![]() �����Σ����
�����Σ����![]() �����꣮
�����꣮
��2�����ı���![]() ��ƽ���ı��Σ���ͼ1����
��ƽ���ı��Σ���ͼ1����![]() ��
��![]() �ֱ�Ϊ
�ֱ�Ϊ![]() ��
��![]() ���е㣬��
���е㣬��![]() ����
����![]() ��ֵ��
��ֵ��
��3�����ı���![]() �Ǿ��Σ���ͼ2����
�Ǿ��Σ���ͼ2����![]() Ϊ�Խ���
Ϊ�Խ���![]() �ϵĶ��㣬
�ϵĶ��㣬![]() Ϊ��
Ϊ��![]() �ϵĶ��㣬��
�ϵĶ��㣬��![]() ����Сֵ��
����Сֵ��
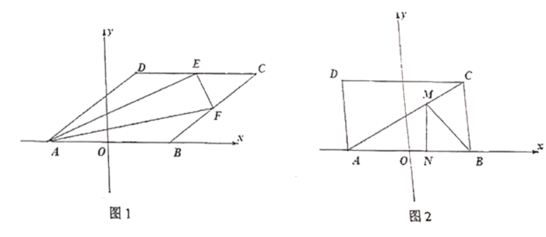
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y��ax2��bx��c��2��ͼ����ͼ��ʾ������Ϊ(��1��0)�����н��ۣ���abc��0����b2��4ac��0����a��2����4a��2b��c��0.������ȷ������____.(�����)
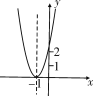
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ABCDλ��ֱ������ϵ�У�AB=2����D��0��1�����Ե�CΪ�����������y=ax2+bx+c����x���������ϵĵ�A��B��CE��x���ڵ�E��
��1�����A��B��C�����꣮
��2����������������ƽ��m����λǡ�þ�����D������ʱ�������߽�x���ڵ�M��N��
����MN�ij���
����P���������߶Գ�����һ���㣬���߶�AP�Ƶ�A˳ʱ����ת60����AQ����OQ����СֵΪ�� ����ֱ��д���𰸼��ɣ�
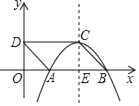
�鿴�𰸺ͽ���>>
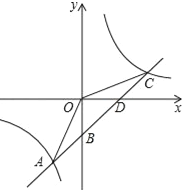
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���y=kx+b��ͼ���뷴��������y=![]() ��ͼ���ڵ�A�v��2����5�w��C�v5��n�w����y���ڵ�B����x���ڵ�D.
��ͼ���ڵ�A�v��2����5�w��C�v5��n�w����y���ڵ�B����x���ڵ�D.
��1����������y=![]() ��һ�κ���y=kx+b�ı���ʽ��
��һ�κ���y=kx+b�ı���ʽ��
��2������OA��OC.���AOC�����.
��3����kx+b��![]() ʱ����д���Ա���x��ȡֵ��Χ.
ʱ����д���Ա���x��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com