|
|
|
如图，在矩形ABCD中，O是AC与BD的交点，过O点的直线EF与AB、CD的延长线分别交于点E、F，连接AF、EC．
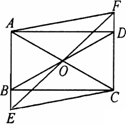
(1)证明：△BOE≌△DOF．
(2)当EF与AC满足什么条件时，四边形AECF是菱形？为什么？
|
|
|
答案：
解析：
|
(1)证明：因为四边形ABCD是矩形，所以AB∥CD，BO＝OD，所以∠BEO＝∠DFO，∠EBO＝∠FDO，所以△BOE≌△DOF．
(2)解：当EF与AC垂直时，四边形AECF是菱形．理由如下：
因为△BOE≌△DOF，所以EO＝FO．
又因为矩形ABCD中，AO＝OC，所以四边形AECF为平行四边形．
又因为EF⊥AC，所以四边形AECF是菱形．
|
练习册系列答案
相关习题
科目：初中数学
来源：新人教版（2012） 八年级下
题型：
|
|
|
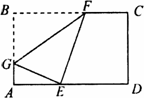
如图，折叠矩形纸片ABCD，使B点落在AD上点E处，折痕的两端点分别在AB、BC上(含端点)，且AB＝6，BC＝10．设AE＝x，则x的取值范围是________．
|
|
|
查看答案和解析>>
科目：初中数学
来源：新人教版（2012） 八年级下
题型：
|
|
|
在□ABCD中，∠A＋∠C＝200°，则∠B的度数是
|
| [ ] |
A． |
100°
|
B． |
160°
|
C． |
80°
|
D． |
60°
|
|
|
查看答案和解析>>
科目：初中数学
来源：新人教版（2012） 八年级下
题型：
|
|
|
如图，在△ABC中，AD是∠BAC的平分线，DE∥AC，DF∥AB．证明：四边形AEDF是菱形．
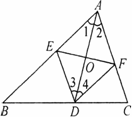
对于这道题，小林是这样证明的．
证明：因为AD平分∠BAC，所以∠1＝∠2．
因为DE∥AC，所以∠2＝∠3．
因为DF∥AB，所以∠1＝∠4．
又AD＝AD，所以△AED≌△AFD．
所以AE＝AF，DE＝DF．
所以四边形AEDF是菱形．
老师说小林的解题过程有错误，你能看出来吗？
(1)请你帮小林指出他的错误是什么．
(2)请你帮小林做出正确的解答．
|
|
|
查看答案和解析>>
科目：初中数学
来源：新人教版（2012） 八年级下
题型：
|
|
|
在平行四边形、菱形、矩形、正方形中，能够找到一点，使该点到各边距离相等的图形是
|
| [ ] |
A． |
平行四边形和菱形
|
B． |
菱形和矩形
|
C． |
矩形和正方形
|
D． |
菱形和正方形
|
|
|
查看答案和解析>>
科目：初中数学
来源：新人教版（2012） 八年级下
题型：
|
|
|
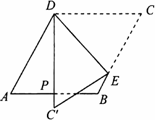
如图，在菱形纸片ABCD中，∠A＝60°，折叠菱形纸片ABCD，使点C落在DP(P为AB中点)所在的直线上，得到经过点D的折痕DE，则∠DEC的大小为
|
| [ ] |
A． |
78°
|
B． |
75°
|
C． |
60°
|
D． |
45°
|
|
|
查看答案和解析>>
科目：初中数学
来源：新人教版（2012） 八年级下
题型：
|
|
|
如图，在□ABCD中，点E，F分别在AB、CD上，且AE＝CF．
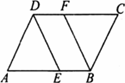
(1)求证：△ADE≌△CBF．
(2)若DF＝BF，求证：四边形DEBF是菱形．
|
|
|
查看答案和解析>>
科目：初中数学
来源：新人教版（2012） 八年级下
题型：
|
|
|
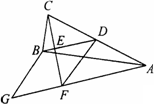
如图，在△ABC中，∠ABC＝90°，BD为AC边上的中线，过点C作CE⊥BD于点E，过点A作BD的平行线，交CE的延长线于点F，在AF的延长线上截取FG＝BD，连接BG、DF．若AG＝13，CF＝6，则四边形BDFG的周长为________．
|
|
|
查看答案和解析>>
科目：初中数学
来源：新人教版（2012） 八年级下
题型：
|
|
|
菱形具有而矩形不一定具有的性质是
|
| [ ] |
A． |
对角线互相垂直
|
B． |
对角线相等
|
C． |
对角线互相平分
|
D． |
对角互补
|
|
|
查看答案和解析>>
