
 如图,图①中圆与正方形各边都相切,设这个圆的周长为C1;图②中的四个圆的半径相等,并依次外切,且与正方形的边相切,设这四个圆的周长为C2;图③中的九个圆的半径相等,并依次外切,且与正方形的边相切,设这九个圆的周长为C3;…,依次规律,当正方形边长为2时,则C1+C2+C3+…C99+C100为( )
如图,图①中圆与正方形各边都相切,设这个圆的周长为C1;图②中的四个圆的半径相等,并依次外切,且与正方形的边相切,设这四个圆的周长为C2;图③中的九个圆的半径相等,并依次外切,且与正方形的边相切,设这九个圆的周长为C3;…,依次规律,当正方形边长为2时,则C1+C2+C3+…C99+C100为( )科目:初中数学 来源: 题型:
| 1 | 2 |
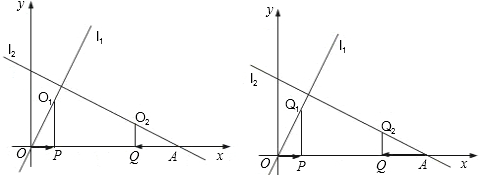 ,求出t值;若不能,说明理由.(同学可在图2中画草图)
,求出t值;若不能,说明理由.(同学可在图2中画草图)查看答案和解析>>
科目:初中数学 来源: 题型:
| k | 3 |
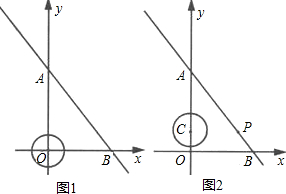 以1个单位/秒的速度运动,设t秒时点P到动圆圆心C的距离为s,求s与t的关系式;
以1个单位/秒的速度运动,设t秒时点P到动圆圆心C的距离为s,求s与t的关系式;查看答案和解析>>
科目:初中数学 来源: 题型:解答题
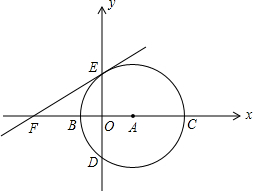 于B、C两点,与y轴相交于D、E两点.
于B、C两点,与y轴相交于D、E两点.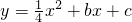 经过C、D两点,求此抛物线的解析式,并判断点B是否在这条抛物线上?
经过C、D两点,求此抛物线的解析式,并判断点B是否在这条抛物线上? ,0),求此直线的解析式,这条直线是⊙A的切线吗?请说明理由;
,0),求此直线的解析式,这条直线是⊙A的切线吗?请说明理由; ?若能,请直接写出Q点坐标;若不能,请说明理由.
?若能,请直接写出Q点坐标;若不能,请说明理由.查看答案和解析>>
科目:初中数学 来源:2012年福建省三明市建宁县初中学业质量检查数学试卷(解析版) 题型:解答题
 经过C、D两点,求此抛物线的解析式,并判断点B是否在这条抛物线上?
经过C、D两点,求此抛物线的解析式,并判断点B是否在这条抛物线上? ,0),求此直线的解析式,这条直线是⊙A的切线吗?请说明理由;
,0),求此直线的解析式,这条直线是⊙A的切线吗?请说明理由; ?若能,请直接写出Q点坐标;若不能,请说明理由.
?若能,请直接写出Q点坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2011年福建省厦门市双十中学中考数学一模试卷(解析版) 题型:解答题
 ,并且与x轴、y轴分别交于点A、B.
,并且与x轴、y轴分别交于点A、B.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com