
【题目】如图,矩形ABCD中,对角线AC与BD相交于点,过点A作AN∥BD,过点B作BN∥AC,两线相交于点N.
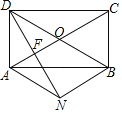
(1)求证:AN=BN;
(2)连接DN,交AC于点F,若DN⊥NB于点N,求∠DOC的度数.
【答案】(1)见解析;(2)120°
【解析】
(1)根据矩形的性质和已知条件可以证明四边形OANB是平行四边形,进而证明OANB是菱形,即可得结论;
(2)结合(1)可以得∠NDB=30°,进而可求∠DOC的度数.
解:(1)证明:∵矩形ABCD中,对角线AC与BD相交于点O,
∴OA=OB,
∵AN∥BD,BN∥AC,
∴四边形OANB是平行四边形,
∵OA=OB,
∴OANB是菱形,
∴AN=BN,
(2)由(1)可知:
BN=OB=OD,
∴BD=2BN,
∵DN⊥NB,
∴∠DNB=90°,
∴∠BDN=30°,
∵BN∥AC,
∴∠DFO=∠DNB=90°,
∴∠DOF=90°﹣30°=60°,
∴∠DOC=180°﹣60°=120°.
答:∠DOC的度数为120°.


科目:初中数学 来源: 题型:
【题目】某水果连锁店销售某种热带水果,其进价为20元/千克.销售一段时间后发现:该水果的日销量![]() (千克)与售价
(千克)与售价![]() (元/千克)的函数关系如图所示:
(元/千克)的函数关系如图所示:
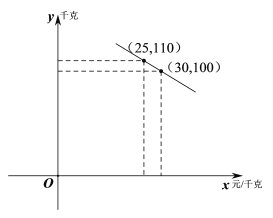
(1)求![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(2)当售价为多少元/千克时,当日销售利润最大,最大利润为多少元?
(3)由于某种原因,该水果进价提高了![]() 元/千克(
元/千克(![]() ),物价局规定该水果的售价不得超过40元/千克,该连锁店在今后的销售中,日销售量与售价仍然满足(1)中的函数关系.若日销售最大利润是
),物价局规定该水果的售价不得超过40元/千克,该连锁店在今后的销售中,日销售量与售价仍然满足(1)中的函数关系.若日销售最大利润是![]() 元,请直接写出
元,请直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如今,不少人在购买家具时追求简约大气的风格,图1所示的是一款非常畅销的简约落地收纳镜,其支架的形状固定不变,镜面可随意调节,图2所示的是其侧面示意图,其中![]() 为镜面,
为镜面,![]() 为放置物品的收纳架,
为放置物品的收纳架,![]() 为等长的支架,
为等长的支架,![]() 为水平地面,已知
为水平地面,已知![]() ,
,![]() .(结果精确到
.(结果精确到![]() .参考数据:
.参考数据:![]() )
)
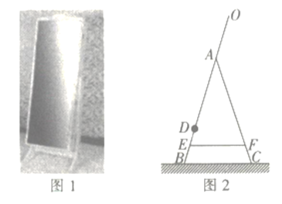
(1)求支架顶点![]() 到地面
到地面![]() 的距离.
的距离.
(2)如图3,将镜面顺时针旋转![]() 求此时收纳镜顶部端点
求此时收纳镜顶部端点![]() 到地面
到地面![]() 的距离.
的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某游泳池每次换水前后水的体积基本保持不变,当该游泳池以每小时300立方米的速度放水时,经3小时能将池内的水放完.设放水的速度为x立方米/时,将池内的水放完需y小时.已知该游泳池每小时的最大放水速度为350立方米
(1)求y关于x的函数表达式.
(2)若该游泳池将放水速度控制在每小时200立方米至250立方米(含200立方米和250立方米),求放水时间y的范围.
(3)该游泳池能否在2.5小时内将池内的水放完?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,航模小组用无人机来测量建筑物BC的高度,无人机从A处测得建筑物顶部B的仰角为45°,测得底部C的俯角为60°,若此时无人机与该建筑物的水平距离AD为30m,则该建筑物的高度BC为_____m.(结果保留根号)
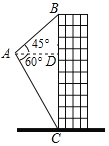
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为调查某市市民上班时最常用的交通工具的情况,随机抽取了部分市民进行调查,要求被调查者从“![]() :自行车,
:自行车,![]() :家庭汽车,
:家庭汽车,![]() :公交车,
:公交车,![]() :电动车,
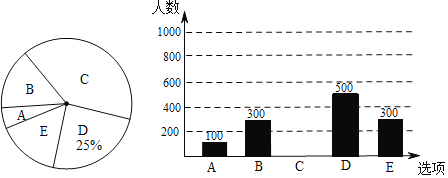
:电动车,![]() :其他”五个选项中选择最常用的一项,将所有调查结果整理后绘制成如下不完整的条形统计图和扇形统计图,请结合统计图回答下列问题:
:其他”五个选项中选择最常用的一项,将所有调查结果整理后绘制成如下不完整的条形统计图和扇形统计图,请结合统计图回答下列问题:
(1)本次调查中,一共调查了 名市民;扇形统计图中,![]() 项对应的扇形圆心角是 °;
项对应的扇形圆心角是 °;
(2)补全条形统计图;
(3)若甲、乙两人上班时从![]() 四种交通工具中随机选择一种,请用列表法或画树状图的方法,求出甲、乙两人恰好选择同一种交通工具上班的概率
四种交通工具中随机选择一种,请用列表法或画树状图的方法,求出甲、乙两人恰好选择同一种交通工具上班的概率
查看答案和解析>>
科目:初中数学 来源: 题型:
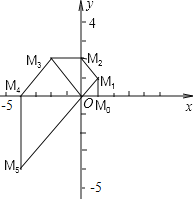
【题目】如图,在平面直角坐标系xOy中,已知点M0的坐标为(1,0),将线段OM0绕原点O逆时针方向旋转45°,再将其延长到M1,使得M1M0⊥OM0,得到线段OM1;又将线段OM1绕原点O逆时针方向旋转45°,再将其延长到M2,使得M2M1⊥OM1,得到线段OM2;如此下去,得到线段OM3,OM4,OM5,…根据以上规律,请直接写出OM2014的长度为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆轿车从甲地驶往乙地,到达乙地后立即返回甲地,速度是原来的![]() 倍,往返共用
倍,往返共用![]() 小时.一辆货车同时从甲地驶往乙地,到达乙地后停止.两车同时出发,匀速行驶,设轿车行驶的时间为
小时.一辆货车同时从甲地驶往乙地,到达乙地后停止.两车同时出发,匀速行驶,设轿车行驶的时间为![]() ,两车离开甲地的距离为
,两车离开甲地的距离为![]() ,两车行驶过程中
,两车行驶过程中![]() 与
与![]() 之间的函数图象如图所示.
之间的函数图象如图所示.
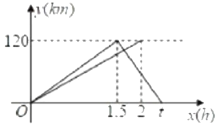
(1)轿车从乙地返回甲地的速度为________![]() ,
,![]() ________;
________;
(2)求轿车从乙地返回甲地时![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)当轿车从乙地返回甲地的途中与货车相遇时,求相遇处到甲地的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境:
我们知道若一个矩形的周长固定,当相邻两边相等,即为正方形时,面积是最大的,反过来,若一个矩形的面积固定,它的周长是否会有最值呢?
方法探究:
用两条直角边分别为![]() 、
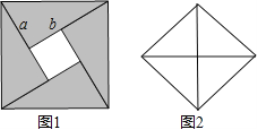
、![]() 的四个全等的直角三角形,可以拼成一个正方形,
的四个全等的直角三角形,可以拼成一个正方形,
若![]() ,可以拼成如图1的正方形,从而得到
,可以拼成如图1的正方形,从而得到![]() ,即
,即![]() ;
;
若![]() ,可以拼成如图2的正方形,从而得到
,可以拼成如图2的正方形,从而得到![]() ,即
,即![]() .
.
于是我们可以得到结论:![]() ,
,![]() 为正数,总有
为正数,总有![]() ,且当
,且当![]() 时,代数式
时,代数式![]() 取得最小值为
取得最小值为![]() .
.
另外,我们也可以通过代数式运算得到类似上面的结论.
∵![]() ,
,
∴![]() ,
,![]() ,
,
∴对于任意实数![]() ,
,![]() ,总有
,总有![]() ,
,
且当![]() 时,代数式
时,代数式![]() 取得最小值为
取得最小值为![]() .
.
类比应用:
(1)对于正数![]() ,
,![]() ,试比较
,试比较![]() 和
和![]() 的大小关系,并说明理由.
的大小关系,并说明理由.
(2)填空:
当![]() 时,
时,![]() ________.
________.
代数式![]() 有最________值为________.
有最________值为________.
问题解决:
(3)若一个矩形的面积固定为![]() ,它的周长是否会有最值呢?若有,求出周长的最值,及此时矩形的长和宽;若没有,请说明理由.
,它的周长是否会有最值呢?若有,求出周长的最值,及此时矩形的长和宽;若没有,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com