
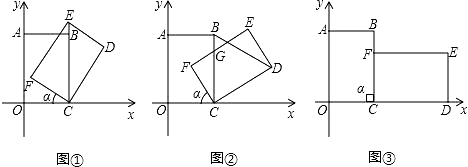
【题目】把边长分别为4和6的矩形ABCO如图放在平面直角坐标系中,将它绕点C顺时针旋转a角,旋转后的矩形记为矩形EDCF.在旋转过程中,
(1)如图①,当点E在射线CB上时,E点坐标为 ;
(2)当△CBD是等边三角形时,旋转角a的度数是 (a为锐角时);
(3)如图②,设EF与BC交于点G,当EG=CG时,求点G的坐标;
(4)如图③,当旋转角a=90°时,请判断矩形EDCF的对称中心H是否在以C为顶点,且经过点A的抛物线上.
【答案】(1)E(4,2![]() )(2)60°(3)
)(2)60°(3)![]() (4)点H不在此抛物线上
(4)点H不在此抛物线上
【解析】
试题分析:(1)依题意得点E在射线CB上,横坐标为4,纵坐标根据勾股定理可得点E.
(2)已知∠BCD=60°,∠BCF=30°,然后可得∠α=60°.
(3)设CG=x,则EG=x,FG=6﹣x,根据勾股定理求出CG的值.
(4)设以C为顶点的抛物线的解析式为y=a(x﹣4)2,把点A的坐标代入求出a值.当x=7时代入函数解析式可得解.
试题解析:(1)E(4,2![]() )
)
(2)60°
(3)设CG=x,则EG=x,FG=6﹣x,
在Rt△FGC中,∵CF2+FG2=CG2,
∴42+(6﹣x)2=x2
解得![]() ,
,
即![]()
∴![]()
(4)设以C为顶点的抛物线的解析式为y=a(x﹣4)2,
把A(0,6)代入,得6=a(0﹣4)2.
解得a=![]()
![]() .
.
∴抛物线的解析式为y=![]() (x﹣4)2
(x﹣4)2
∵矩形EDCF的对称中心H即为对角线FD、CE的交点,
∴H(7,2).
当x=7时,![]()
∴点H不在此抛物线上.


科目:初中数学 来源: 题型:
【题目】一个三位数,百位数字为a,十位数字为b,个位数字为c,这个三位数可以表示为( )
A. abc B. 100b+10a+c C. cba D. 100a+10b+c
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自主学习,请阅读下列解题过程.
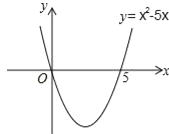
解一元二次不等式:x2﹣5x>0.
解:设x2﹣5x=0,解得:x1=0,x2=5,则抛物线y=x2﹣5x与x轴的交点坐标为(0,0)和(5,0).画出二次函数y=x2﹣5x的大致图象(如图所示),由图象可知:当x<0,或x>5时函数图象位于x轴上方,此时y>0,即x2﹣5x>0,所以,一元二次不等式x2﹣5x>0的解集为:x<0或x>5.
通过对上述解题过程的学习,按其解题的思路和方法解答下列问题:
(1)上述解题过程中,渗透了下列数学思想中的 和 .(只填序号)
①转化思想 ②分类讨论思想 ③数形结合思想
(2)一元二次不等式x2﹣5x<0的解集为 .
(3)用类似的方法写出一元二次不等式的解集:x2﹣2x﹣3>0. .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AB的垂直平分线交AB于M,交AC于N.
(1)若∠ABC=70°,求∠MNA的度数.
(2)连接NB,若AB=8cm,△NBC的周长是14cm.求BC的长;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市出租车收费方式如下:行驶距离在3 km以内(包括3 km)付起步价5元,超过3 km后,每多行驶1 km加收2元.则乘车费用y(元)与乘车距离x(km)(x>3)之间的函数解析式为____________(不需要写出自变量的取值范围).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com